题目内容
设函数f(x)=2sinωxsin(ωx+
)+k(ω>0,k为常数).
(1)若f(x)的图象中相邻两对称轴之间的距离不小于
,求ω的取值范围;
(2)若f(x)的最小正周期为π,且当x∈[-
,
]时,f(x)的最大值是
,又f(α)=
,求f(
-α)的值.
| π |
| 3 |
(1)若f(x)的图象中相邻两对称轴之间的距离不小于
| π |
| 2 |
(2)若f(x)的最小正周期为π,且当x∈[-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)利用两角和与差的三角函数化简函数的表达式为一个角的一个三角函数的形式,利用函数的周期的一半不小于
,即可求ω的取值范围;
(2)通过f(x)的最小正周期为π,求出函数的解析式,通过x∈[-
,
]完成相位的范围,然后通过求解f(x)的最大值是
,又f(α)=
,利用两角和与差的三角函数求f(
-α)的值.
| π |
| 2 |
(2)通过f(x)的最小正周期为π,求出函数的解析式,通过x∈[-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
解答:
解:(1)f(x)=2sinωxsin(ωx+
)+k
=sin2ωx+
sinωxcosωx+k
=
sin2ωx+
+k
=sin(2ωx-
)+k+
…(6分)
由题意知
≥
,得ω的取值范围为0<ω≤1 …(8分)
(2)若f(x)的最小正周期为π,得ω=1 …(9分)
f(x)=sin(2x-
)+k+
,有f(x)在区间[-
,
]上为增函数,
所以f(x)的最大值为f(
)=1+k=
,则k=-
,…(11分)
所以f(α)=sin(2α-
)=
,所以cos(2α-
)=±
…(12分)
f(
-α)=sin(2α+
)
=sin(2α-
+
)
=
sin(2α-
)+
cos(2α-
)
=
或
…(14分)
| π |
| 3 |
=sin2ωx+
| 3 |
=
| ||
| 2 |
| 1-cos2ωx |
| 2 |
=sin(2ωx-
| π |
| 6 |
| 1 |
| 2 |
由题意知
| T |
| 2 |
| π |
| 2 |
(2)若f(x)的最小正周期为π,得ω=1 …(9分)
f(x)=sin(2x-
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
所以f(x)的最大值为f(
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
所以f(α)=sin(2α-
| π |
| 6 |
| 3 |
| 5 |
| π |
| 6 |
| 4 |
| 5 |
f(
| π |
| 2 |
| π |
| 6 |
=sin(2α-
| π |
| 6 |
| π |
| 3 |
=
| 1 |
| 2 |
| π |
| 6 |
| ||
| 2 |
| π |
| 6 |
=
3+4
| ||
| 10 |
3-4
| ||
| 10 |
点评:本题考查三角函数的化简求值,两角和与差的三角函数的应用,三角函数的基本性质的应用,考查计算能力.

练习册系列答案
相关题目
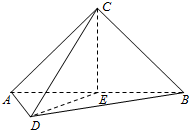 如图,在三棱锥C-ABD中,AC⊥CB,AC=CB,E为AB的中点,AD=DE=EC=2,CD=2
如图,在三棱锥C-ABD中,AC⊥CB,AC=CB,E为AB的中点,AD=DE=EC=2,CD=2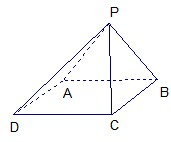 已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=
已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP= 已知A、B、C、D四点不共面,M、N分别是△ABD和△BCD的重心.求证:MN∥平面ACD.
已知A、B、C、D四点不共面,M、N分别是△ABD和△BCD的重心.求证:MN∥平面ACD.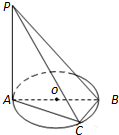 如图,AB是圆O的直径,PA垂直于圆所在的平面,C是圆周上的点.
如图,AB是圆O的直径,PA垂直于圆所在的平面,C是圆周上的点.