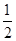题目内容
设等差数列 的前
的前 项和为
项和为 ,且
,且 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前
的前 项和为
项和为 ,且
,且 (
( 为常数),令
为常数),令 ,求数列
,求数列 的前
的前 项和
项和 。
。
 的前
的前 项和为
项和为 ,且
,且 ,
, .
.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)设数列
 的前
的前 项和为
项和为 ,且
,且 (
( 为常数),令
为常数),令 ,求数列
,求数列 的前
的前 项和
项和 。
。(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
(Ⅰ)设等差数列 的公差为
的公差为 ,则
,则
 ,解得
,解得 ,
,
所以
(Ⅱ)由(Ⅰ)得 ,所以
,所以 .
.


当 时,
时,
因此
所以

相减得
 ,
,

化简得
【考点定位】本题从等差数列的基本问题(首项、公差、通项公式)入手,通过新数列的构造考查了 与
与 的关系、错位相减法求和等,涉及等比数列的求和公式的应用、代数式的化简等,是对运算能力的有力考查.
的关系、错位相减法求和等,涉及等比数列的求和公式的应用、代数式的化简等,是对运算能力的有力考查.
 的公差为
的公差为 ,则
,则 ,解得
,解得 ,
,所以

(Ⅱ)由(Ⅰ)得
 ,所以
,所以 .
.

当
 时,
时,
因此

所以


相减得

 ,
,
化简得

【考点定位】本题从等差数列的基本问题(首项、公差、通项公式)入手,通过新数列的构造考查了
 与
与 的关系、错位相减法求和等,涉及等比数列的求和公式的应用、代数式的化简等,是对运算能力的有力考查.
的关系、错位相减法求和等,涉及等比数列的求和公式的应用、代数式的化简等,是对运算能力的有力考查.
练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
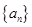 的前n项和为
的前n项和为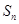 ,若
,若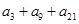 的值为常数,则下列各数中也是常数的是( ).
的值为常数,则下列各数中也是常数的是( ). 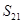
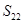

 S
S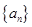 中,
中,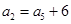 ,则其公差为 .
,则其公差为 . 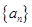 的前三项依次为
的前三项依次为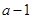 ,
,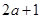 ,
,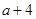 ,则
,则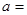 .
. ,一直数到2013时,对应的指头是 (填指头的名称).
,一直数到2013时,对应的指头是 (填指头的名称). 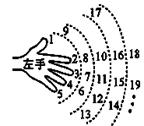
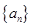 是递增数列,
是递增数列,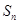 是
是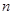 项和。若
项和。若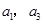 是方程
是方程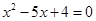 的两个根,则
的两个根,则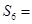 .
.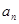 }的前n项和为
}的前n项和为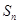 ,
,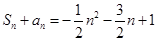 ,
,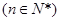 .
.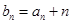 ,证明:数列
,证明:数列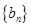 是等比数列;
是等比数列;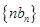 的前
的前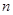 项和
项和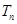 ;
; ,
, ,
, ,记
,记
 ,
,
 ,
,
 (
( ),若对于任意
),若对于任意 ,
, ,
, 成等差数列.
成等差数列. 的前
的前 项和.
项和.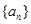 为等差数列,且
为等差数列,且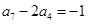 ,
,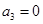 ,则公差
,则公差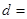 ( )
( )