题目内容
(12分)已知向量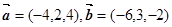
(1)求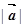 ;(2)求
;(2)求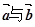 夹角的余弦值.
夹角的余弦值.
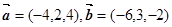
(1)求
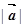 ;(2)求
;(2)求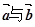 夹角的余弦值.
夹角的余弦值.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.本试题主要考查了向量的数量积公式的运用,以及夹角公式的运算。
第一问中,因为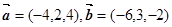 ,则
,则

第二问中,因为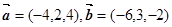
所以
利用夹角公式求解得到。
(1) 因为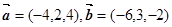 ,则
,则

(2)因为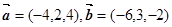
所以

故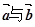 夹角的余弦值为
夹角的余弦值为
第一问中,因为
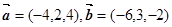 ,则
,则
第二问中,因为
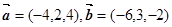
所以

利用夹角公式求解得到。
(1) 因为
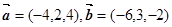 ,则
,则
(2)因为
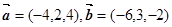
所以

故
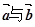 夹角的余弦值为
夹角的余弦值为

练习册系列答案
相关题目
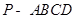 中,
中,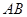 //
//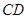 ,
,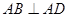 ,
,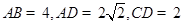 ,
,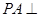 平面
平面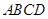 ,
,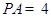 .
. 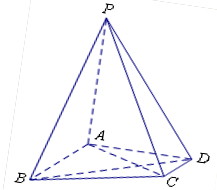
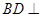 平面
平面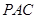 ;
;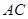 与
与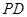 所成角的余弦值;
所成角的余弦值; 为线段
为线段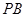 上一点,且直线
上一点,且直线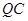 与平面
与平面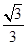 ,求
,求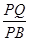 的值.
的值. 的对角线
的对角线 上一点,记
上一点,记 .当
.当 为钝角时,则
为钝角时,则 的取值范围为( )
的取值范围为( )



 =
= ,则向量
,则向量 的坐标为 。
的坐标为 。 则
则 到平面
到平面 的距离是
的距离是 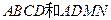 边长都为2,且
边长都为2,且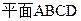
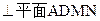 ,
,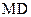 的中点,
的中点,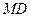
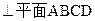 。(2分)
。(2分)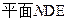 的距离。(5分)
的距离。(5分)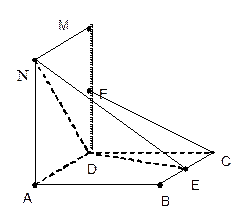
 ,
, ,
, ,则
,则 与
与 的值分别为( ).
的值分别为( ).



 ,若
,若
 ,则
,则 ______
______ ,且
,且 ,则实数
,则实数 的值是
的值是