题目内容
如图,已知正方体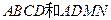 边长都为2,且
边长都为2,且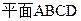
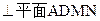 ,
,
E是BC的中点,F是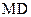 的中点,
的中点,
(1)求证: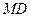
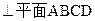 。(2分)
。(2分)
(2)求点A到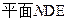 的距离。(5分)
的距离。(5分)
(3)求证:CF∥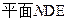 。(3分)
。(3分)
(4) 求二面角E-ND-A的平面角大小的
余弦值。(4分)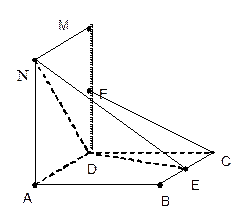
 边长都为2,且
边长都为2,且
 ,
,E是BC的中点,F是
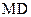 的中点,
的中点,(1)求证:
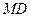
 。(2分)
。(2分)(2)求点A到
 的距离。(5分)
的距离。(5分)(3)求证:CF∥
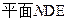 。(3分)
。(3分)(4) 求二面角E-ND-A的平面角大小的
余弦值。(4分)

解:(1)∵平面ABCD
 .
.


∴
 MD
MD
------------2分
(2) 分别以DA,DC,DM为x轴,y轴,z轴建立空间直角坐标系,则A(2,0,0), N(2,0,2),E(1,2,0),D(0,0,0), C(0,2,0), F(0,0,1), ------4分
则

设平面NDE的法向量是
 则
则  ,
, 取b="1. " 则
 ------------6分
------------6分∴点A到平面NDE的距离是
 。----------7分
。----------7分(2)
 ,
, ,
,∴ CF∥平面NDE。------------10分
(3)
 是面AND的法向量,
是面AND的法向量,  。------------12分
。------------12分∵ 二面角E-ND-A为锐角------------13分
∴ 二面角E-ND-A的平面角大小的余弦值为
 。---------14分
。---------14分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
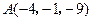 ,
,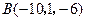 ,
,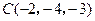 为顶点的三角形是等腰直角三角形.
为顶点的三角形是等腰直角三角形.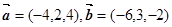
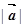 ;(2)求
;(2)求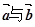 夹角的余弦值.
夹角的余弦值. 为单位正交基,且
为单位正交基,且 ,则向量
,则向量 与向量
与向量 的坐标分别是______________;_________________.
的坐标分别是______________;_________________.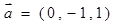 ,
,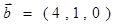 ,
, 且
且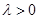 ,则
,则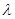 = ____________.
= ____________. 的一个法向量的是( )
的一个法向量的是( )






 =(1-t,1-t,t),
=(1-t,1-t,t), =(2,t,t),则|
=(2,t,t),则|