题目内容
19.在平面直角坐标系xOy中,直线l的参数方程$\left\{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为:ρ=4cosθ.(Ⅰ)直线l的参数方程化为极坐标方程;
(Ⅱ)求直线l与曲线C交点的极坐标(其中ρ≥0,0≤θ≤2π).
分析 (Ⅰ)消去参数t,求出直线l的普通方程,由此能求出直线l的极坐标方程.
(Ⅱ)求出曲线C的直角坐标方程,从而求出直线l与曲线C交点的直角坐标,由此能求出直线l与曲线C交点的极坐标.
解答 解:(Ⅰ)∵直线l的参数方程$\left\{\begin{array}{l}{x=2+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数),
∴消去参数t,得直线l的普通方程为$\sqrt{3}x-y-2\sqrt{3}$=0,
∴直线l的极坐标方程为$\sqrt{3}ρcosθ-ρsinθ-2\sqrt{3}$=0.
(Ⅱ)∵曲线C的极坐标方程为:ρ=4cosθ,∴ρ2=4ρcosθ,
∴曲线C的直角坐标方程为x2+y2-4x=0,
联立$\left\{\begin{array}{l}{\sqrt{3}x-y-2\sqrt{3}=0}\\{{x}^{2}+{y}^{2}-4x=0}\end{array}\right.$,得x2-4x+3=0,
解得x1=1,x2=3,
∴直线l与曲线C交点的直角坐标为(1,-$\sqrt{3}$),(3,$\sqrt{3}$),
∴直线l与曲线C交点的极坐标为(2,$\frac{5π}{3}$),(2$\sqrt{3}$,$\frac{π}{6}$).
点评 本题考查直线的极坐标方程的求法,考查直线与曲线交点的极坐标的求法,是中档题,解题时要认真审题,注意极坐标和直角坐标互化公式的合理运用.

练习册系列答案
相关题目
10.图中的几何体是下列图中的( )绕线旋转一周得到的.


| A. |  | B. |  | C. |  | D. |  |
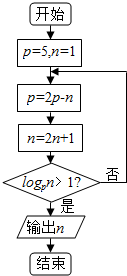
7.如图是一个程序框图,则输出的n的值是 ( )

| A. | 29 | B. | 31 | C. | 61 | D. | 63 |
14.在框图中,设x=2,并在输入框中输入n=4;ai=i(i=0,1,2,3,4).则此程序执行后输出的S值为( )


| A. | 26 | B. | 49 | C. | 52 | D. | 98 |
9.已知sinα=3cosα,则sinα•cosα的值为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{15}$ | D. | $\frac{7}{20}$ |
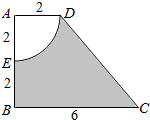 如图所示,直角梯形ABCD(单位cm),ADE为扇形,则图中阴影部分绕AB所在直线旋转一周所形成的几何体体积64πcm3.
如图所示,直角梯形ABCD(单位cm),ADE为扇形,则图中阴影部分绕AB所在直线旋转一周所形成的几何体体积64πcm3.