题目内容
7.在(1+2x-$\frac{1}{{x}^{2016}}$)10的展开式中,x2项的系数为180.分析 (1+2x-$\frac{1}{{x}^{2016}}$)10的展开式中,通项公式Tr+1=${∁}_{10}^{r}$$(1+2x)^{10-r}(-\frac{1}{{x}^{2016}})^{r}$,令r=0,可得:T1=(1+2x)10,再考虑其通项公式即可得出.
解答 解:(1+2x-$\frac{1}{{x}^{2016}}$)10的展开式中,通项公式Tr+1=${∁}_{10}^{r}$$(1+2x)^{10-r}(-\frac{1}{{x}^{2016}})^{r}$,
必须令r=0,可得:T1=(1+2x)10,
其中(1+2x)10的展开式的通项公式:Tk+1=${∁}_{10}^{k}$(2x)k=${2}^{k}{∁}_{10}^{k}{x}^{k}$,
令k=2,可得x2项的系数为${2}^{2}{∁}_{10}^{2}$.
∴在(1+2x-$\frac{1}{{x}^{2016}}$)10的展开式中,x2项的系数=${2}^{2}{∁}_{10}^{2}$=180.
故答案为:180.
点评 本题考查了二项式定理的应用、组合数的计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x-1},x≥1}\\{1,x<1}\end{array}\right.$,则f(5)=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不存在 |
6.已知离心率为2的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的实轴长为8,则该双曲线的渐近线方程为( )
| A. | y=±$\sqrt{3}$x | B. | y=±$\sqrt{2}$x | C. | y=±$\frac{\sqrt{3}}{3}$x | D. | y=±$\frac{\sqrt{2}}{2}$x |
7.若直线y=2x与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1没有公共点,则双曲线的离心率的取值范围是( )
| A. | [$\sqrt{3}$,+∞) | B. | [$\sqrt{5}$,+∞) | C. | (1,$\sqrt{3}$] | D. | (1,$\sqrt{5}$] |
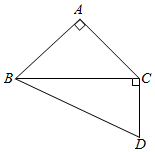 如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.
如图,△ABC是等腰直角三角形,AB=AC,∠BCD=90°,且BC=$\sqrt{3}$CD=3.将△ABC沿BC的边翻折,设点A在平面BCD上的射影为点M,若点M在△BCD内部(含边界),则点M的轨迹的最大长度等于$\frac{\sqrt{3}}{2}$;在翻折过程中,当点M位于线段BD上时,直线AB和CD所成的角的余弦值等于$\frac{\sqrt{6}}{6}$.