题目内容
19.函数f(x)=x+sinx在$x=\frac{π}{2}$处的切线与两坐标轴围成的三角形面积为$\frac{1}{2}$.分析 求出函数的导数,可得切线的斜率,可得切线的方程,求得x,y轴的截距,运用三角形的面积公式,计算即可得到所求值.
解答 解:f(x)=x+sinx,则f'(x)=1+cosx,
∴f'($\frac{π}{2}$)=1,而f($\frac{π}{2}$)=$\frac{π}{2}$+1,
故切线方程为y-($\frac{π}{2}$+1)=x-$\frac{π}{2}$.
令x=0,可得y=1;令y=0,可得x=-1.
故切线与两坐标围成的三角形面积为$\frac{1}{2}×1×1$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,以及直线方程的运用,正确求导是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设X是一个离散型随机变量,则下列不能成为X的概率分布列的一组数据是( )
| A. | 0,$\frac{1}{2}$,0,0,$\frac{1}{2}$ | B. | 0.1,0.2,0.3,0.4 | ||
| C. | p,1-p(0≤p≤1) | D. | $\frac{1}{1×2}$,$\frac{1}{2×3}$,…,$\frac{1}{7×8}$ |
4.如图为体积是3的几何体的三视图,则正视图的x值是( )
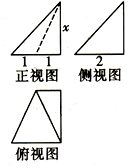

| A. | 2 | B. | $\frac{9}{2}$ | C. | $\frac{3}{2}$ | D. | 3 |
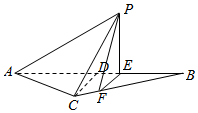 等腰△ABC的底边$AB=6\sqrt{6}$,高CD=3,点E是线段BD上异于点B,D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
等腰△ABC的底边$AB=6\sqrt{6}$,高CD=3,点E是线段BD上异于点B,D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.