Question

2．若△OAB是以O为直角顶点的三角形，且面积为$\frac{\sqrt{6}}{2}$，设向量$\overrightarrow{a}$=$\frac{\overrightarrow{OA}}{|\overrightarrow{OA}|}$，$\overrightarrow{b}$=$\frac{\overrightarrow{OB}}{|\overrightarrow{OB}|}$，$\overrightarrow{OP}$=2$\overrightarrow{a}$+3$\overrightarrow{b}$，则$\overrightarrow{PA}$•$\overrightarrow{PB}$的最大值为13-2$\sqrt{6\sqrt{6}}$．

Answer 1

分析 以OA所在的直线为x轴，OB所在的直线为y轴建立直角坐标系，设点A（m，0）、B（0，n），由S_△OAB=$\frac{1}{2}$mn=$\frac{\sqrt{6}}{2}$可得mn的值，从而利用不等式可求得$\overrightarrow{PA}$•$\overrightarrow{PB}$的最大值．

解答 解：以OA所在的直线为x轴，OB所在的直线为y轴建立直角坐标系，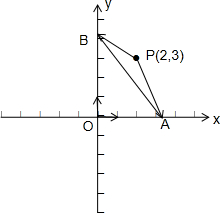

则$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（0，1），P（2，3），
设A（m，0），B（0，n），则m＞0，n＞0．
故$\overrightarrow{PA}$=（m-2，-3），$\overrightarrow{PB}$=（-2，n-3），
又S_△OAB=$\frac{1}{2}$mn=$\frac{\sqrt{6}}{2}$，
所以mn=$\sqrt{6}$．
故$\overrightarrow{PA}$•$\overrightarrow{PB}$=-2（m-2）-3（n-3）=13-（2m+3n）≤13-2$\sqrt{6mn}$（当且仅当2m=3n，即n=$\sqrt{\frac{2\sqrt{6}}{3}}$时取“=”）．
所以，$\overrightarrow{PA}$•$\overrightarrow{PB}$≤13-2$\sqrt{6\sqrt{6}}$．
故答案为：13-2$\sqrt{6\sqrt{6}}$．

点评 本题考查平面向量数量积的运算，以OA为x轴，OB为y轴建立直角坐标系是关键，考查平面向量的坐标运算与基本不等式的应用，属于中档题．