题目内容
6.已知($\sqrt{x}$+$\frac{2}{\sqrt{x}}$)n展开式中第二、三、四项的二项式系数成等差数列.(Ⅰ)求n的值;
(Ⅱ)此展开式中是否有常数项?为什么?
分析 (Ⅰ)先求得($\sqrt{x}$+$\frac{2}{\sqrt{x}}$)n展开式中第二、三、四项的二项式系数,再根据这3个系数成等差数列,求得n的值.
(Ⅱ)在二项展开式的通项公式中,令x的幂指数等于零,得到r的值不是非负整数,可得展开式无常数项.
解答 解:(Ⅰ)由于($\sqrt{x}$+$\frac{2}{\sqrt{x}}$)n展开式中第二、三、四项的二项式系数分别为${C}_{n}^{1}$,${C}_{n}^{2}$,${C}_{n}^{3}$,
由题意可得:2${C}_{n}^{2}$=${C}_{n}^{1}$+${C}_{n}^{3}$,解得n=7.
(Ⅱ) ${(\sqrt{x}+\frac{2}{{\sqrt{x}}})^7}$展开式的通项公式为${T_{r+1}}=C_7^r{(\sqrt{x})^{7-r}}{(\frac{2}{{\sqrt{x}}})^r}={2^r}C_7^r{x^{\frac{7-2r}{2}}}$,
令$\frac{7-2r}{2}=0$,解得$r=\frac{7}{2}$(舍去),故展开式无常数项.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.如图是一个结构图,在框②中应填入( )
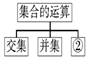

| A. | 空集 | B. | 补集 | C. | 子集 | D. | 全集 |
1.在以“菊韵荆门,荣耀中华”为主题的“中国•荆门菊花展”上,工作人员要将6盆不同品种的菊花排成一排,其中甲,乙在丙同侧的不同排法种数为( )
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
18.设点F1、F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点(O为坐标原点),以O为圆心,|F1F2|为直径的圆交双曲线于点M(第一象限).若过点M作x轴的垂线,垂足恰为线段OF2的中点,则双曲线的离心率是( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | 2 |
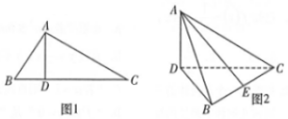 如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.
如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.