题目内容
2.数列{an}的前n项和为Sn,a1=1,Sn=2an+1(n∈N*).(1)试求a2,a3的值及数列{an}的通项公式;
(2)求数列{$\frac{1}{{a}_{n}}$}的前n项和Tn.
分析 (1)利用递推关系与等比数列的通项公式即可得出;
(2)n=1时,T1=1.当n≥2时,$\frac{1}{{a}_{n}}$=$2(\frac{2}{3})^{n-2}$,再利用等比数列的前n项和公式即可得出.
解答 解:(1)∵a1=1,Sn=2an+1(n∈N*),
∴当n=1时,1=a1=2a2,解得a2=$\frac{1}{2}$;
当n=2时,a1+a2=2a3,即1+$\frac{1}{2}$=2a3,解得a3=$\frac{3}{4}$.
当n≥2时,an=Sn-Sn-1=2an+1-2an,化为an+1=$\frac{3}{2}{a}_{n}$.
∴当n≥2时,数列{an}是等比数列,公比为$\frac{3}{2}$,
∴${a}_{n}=\frac{1}{2}×(\frac{3}{2})^{n-2}$.
∴an=$\left\{\begin{array}{l}{1,n=1}\\{\frac{1}{2}(\frac{3}{2})^{n-2},n≥2}\end{array}\right.$.
(2)n=1时,T1=1.
当n≥2时,$\frac{1}{{a}_{n}}$=$2(\frac{2}{3})^{n-2}$,
∴Tn=1+2×$\frac{1-(\frac{2}{3})^{n-1}}{1-\frac{2}{3}}$=7-$6×(\frac{2}{3})^{n-1}$.n=1时也成立.
∴Tn=7-$6×(\frac{2}{3})^{n-1}$.
点评 本题考查了递推关系、等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
7.若函数f(x)=1+$\frac{a}{{a}^{x}-1}$是奇函数,则a的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
19.某几何体的三视图如图所示,则该几何体的体积为( )
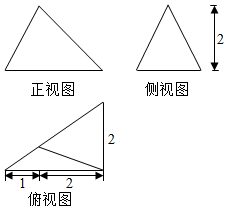

| A. | $\frac{4}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 3 | D. | 2 |