题目内容
已知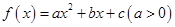 ,当
,当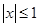 时,
时,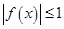 .
.
(1)证明: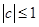 ;
;
(2)若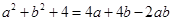 成立,请先求出
成立,请先求出 的值,并利用
的值,并利用 值的特点求出函数
值的特点求出函数 的表达式.
的表达式.
(1)详见解析;(2)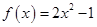 .
.
解析试题分析:(1)根据题中条件并利用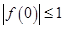 得到
得到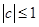 ;(2)先利用题中条件得到
;(2)先利用题中条件得到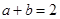 ,并结合
,并结合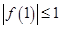 得到
得到 的取值范围,结合(1)中的结论求出
的取值范围,结合(1)中的结论求出 值,然后借助题中条件分析出函数是
值,然后借助题中条件分析出函数是 的图象关于
的图象关于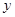 轴对称,从而求出
轴对称,从而求出 与
与 的值,从而最终确定函数
的值,从而最终确定函数 的解析式.
的解析式.
试题解析:(1)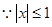 时
时 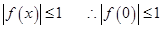
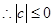 4分
4分
(2)由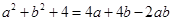 得到
得到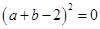
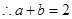 5分
5分
又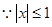 时
时 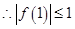 即
即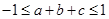
将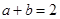 代入上式得
代入上式得 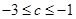 又
又 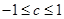
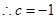 8分
8分
又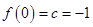
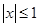 时
时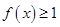
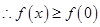
对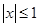 均成立
均成立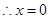 为函数
为函数 为对称轴 10分
为对称轴 10分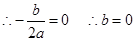 又
又
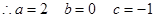 12分
12分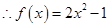 13分
13分
考点:1.函数不等式;2.二次函数的对称性

练习册系列答案
相关题目
 的定义域为
的定义域为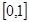 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:①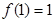 ;②对任意的
;②对任意的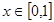 ,都有
,都有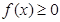 ;③当
;③当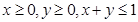 时总有
时总有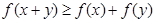 .
.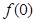 的值;
的值;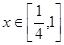 时,恒有
时,恒有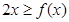 .
. 为实数,函数
为实数,函数 。
。 ,求
,求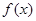 的最小值;
的最小值;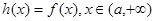 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式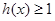 的解集.
的解集.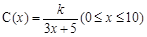 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和. 为偶函数,且在区间
为偶函数,且在区间 上是单调增函数
上是单调增函数 的解析式;
的解析式; ,其中
,其中 .若函数
.若函数 仅在
仅在 处有极值,求
处有极值,求 的取值范围.
的取值范围. .若
.若 的定义域为
的定义域为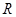 ,求实数
,求实数 的取值范围.
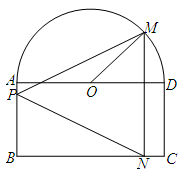
的取值范围.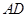 为半圆的直径,
为半圆的直径,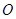 为半圆的圆心,
为半圆的圆心, ,
,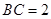 ,现要将此铁皮剪出一个等腰三角形
,现要将此铁皮剪出一个等腰三角形 ,其底边
,其底边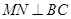 .
.
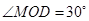 ,求三角形铁皮
,求三角形铁皮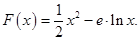
 的最小值;
的最小值;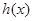 和
和 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数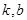 ,使得不等式
,使得不等式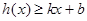 和
和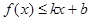 都成立,则称直线
都成立,则称直线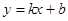 是函数
是函数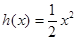 ,
,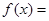
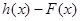 ,试问函数
,试问函数