题目内容
已知圆C:(x-3)2+(y-4)2=1和点A(-1,0),B(1,0),点P在⊙C上运动.求PA2+PB2的最大(小)值及相应的P点坐标.
考点:直线和圆的方程的应用
专题:计算题,数形结合
分析:设P点坐标为(x0,y0),计算PA2+PB2的值,利用Z=x02+y02的意义即圆上的点到原点的距离的平方,
数形结合,求PA2+PB2的最大值和最小值,并求相应的点P的坐标.
数形结合,求PA2+PB2的最大值和最小值,并求相应的点P的坐标.
解答:
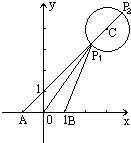 解:如图,设P点坐标为(x0,y0),
解:如图,设P点坐标为(x0,y0),
则PA2+PB2=(x0+1)2 +y02 +(x0-1)2 +y02=2(x02+y02)+2
令Z=x02+y02,显然Z表示圆C上一点到原点的距离的平方,
当Z最大(小)时,PA2+PB2最大(小),设直线OC交圆C于两点P1,P2,
当P与P1重合时,Z最小,其值为(|OC|-1)2=16
当P与P2重合时,Z最大,其值为(|OC|+1)2=36
∴PA2+PB2的最大值为74,最小值为34.
直线OC的方程为y=
x,解方程组
台得P1(
,
),P2(
,
) 即相应的点P的坐标.
 解:如图,设P点坐标为(x0,y0),
解:如图,设P点坐标为(x0,y0),则PA2+PB2=(x0+1)2 +y02 +(x0-1)2 +y02=2(x02+y02)+2
令Z=x02+y02,显然Z表示圆C上一点到原点的距离的平方,
当Z最大(小)时,PA2+PB2最大(小),设直线OC交圆C于两点P1,P2,
当P与P1重合时,Z最小,其值为(|OC|-1)2=16
当P与P2重合时,Z最大,其值为(|OC|+1)2=36
∴PA2+PB2的最大值为74,最小值为34.
直线OC的方程为y=
| 4 |
| 3 |
|
台得P1(
| 12 |
| 5 |
| 16 |
| 5 |
| 18 |
| 5 |
| 24 |
| 5 |
点评:本题考查直线、点与圆的位置关系的应用,注意式子Z=x02+y02表示的意义,体现数形结合的数学思想,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
设函数f(x)=
x3-mx2+(m2-4)x,x∈R,当m=3时,则曲线y=f(x)在点(2,f(2))处的切线方程为( )
| 1 |
| 3 |
| A、9x+3y-20=0 |
| B、9x+3y-2=0 |
| C、9x+3y-10=0 |
| D、9x+3y+20=0 |
直线l与平面a内的两条直线都垂直,则直线l与平面a的位置关系是( )
| A、平行 | B、垂直 |
| C、在平面a内 | D、无法确定 |

 如图所示,向正方形任意抛掷一点,此点不落在阴影部分的概率是
如图所示,向正方形任意抛掷一点,此点不落在阴影部分的概率是 ,其中常数
,其中常数 .
.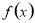 的单调区间及单调性;
的单调区间及单调性;  时
时 恒成立,求实数
恒成立,求实数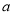 的取值范围.
的取值范围.
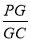 的值.
的值.