题目内容

求函数y=2sinx+1的最大值、最小值和最小正周期．
考点：三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：利用y=sinx的周期以及最值解答本题．
解答： 解：当sinx=1时，y的最大值为2+1=3，；当sinx=-1时，y的最小值为-2+1=-1；
最小正周期为2π．
点评：本题考查了三角函数的最值以及周期的求法；y=Asinx+k的最大值为|A|+k，最小值为-|A|+k；最小正周期为2π．
练习册系列答案
相关题目
函数f（x）=x+
1
2x+1
的定义域为
 
．
已知函数f（x）=x（a+lnx）有极小值-e-2．
（1）求实数a的值；
（2）若k∈Z，且k＜
f(x)
x-1
对任意x＞1恒成立，求k的最大值；
（3）当n＞m＞1，（n，m∈Z）时，证明：（mnn）m＞（nmm）n．
设f（x）定义域为R，x＞0时f（x）＞1且对任意x，y∈R，有f（x+y）=f（x）•f（y），
（1）求f（0）；
（2）判断其单调性并证明．
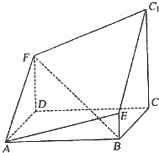如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的，其中AB=4，BC=2，CC1=3，BE=1
（Ⅰ）求BF的长；
（Ⅱ）求面AEC1F与底面ABCD所成二面角的余弦值
（Ⅲ）求点C到平面AEC1F的距离．
解下列不等式．
（1）3x2-x-4＞0；
（2）x2-x-12≤0．
函数f（x）=x-4
x
+m，当0≤x≤9时，f（x）≥1恒成立，则实数m的取值范围为
 
．
已知向量
a
=（1，n），
b
=（-1，n），若2
a
+
b
与
b
垂直，则|
a
|=（　　）
A、1
B、
2
C、
2
3
3
D、4
已知关于x的对数1gx=31gn-1gm，求x的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网