题目内容
△OAB中,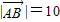
(1)点C为直线AB上一点,且
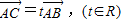 ,试用
,试用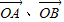 表示
表示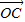 .
.(2)点C1、C2,…,C9依次为线段AB的10等分点,且
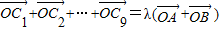 ,求实数λ的值.
,求实数λ的值.(3)条件同(2),又点P为线段AB上一个动点,定义关于点P的函数
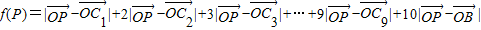 ,求f(P)的最小值.
,求f(P)的最小值.
【答案】分析:(1)根据向量减法的三角形法则,可得 =
= -
- ,再由
,再由 ,
, =
= +
+ 可得答案;
可得答案;
(2)根据向量定比分点公式,当C将AB分为长度比为a:b的两段时, =
= ,逐一求出各分点对应的向量累加可得答案.
,逐一求出各分点对应的向量累加可得答案.
(3)设 =x
=x ,则
,则 =|x-1|+2|x-2|+3|x-3|+…+9|x-9|+10|x-10|利用零点分段法化简函数的解析式,并结合一次函数的图象和性质分析函数的单调性,可得函数的最小值.
=|x-1|+2|x-2|+3|x-3|+…+9|x-9|+10|x-10|利用零点分段法化简函数的解析式,并结合一次函数的图象和性质分析函数的单调性,可得函数的最小值.
解答:解:(1)在△OAB中 =
= -
-
∴ =t
=t -t
-t
∴ =
= +
+ =t
=t +(1-t)
+(1-t)
(2)∵C1、C2,…,C9依次为线段AB的10等分点,
∴ =
=
 +
+
 ;
;
 =
=
 +
+
 ;
;
…
 =
=
 +
+
 ;
;
…
 =
=
 +
+
 ;
;
∴ =(
=( +
+ +…+
+…+ )
) =
=

故λ=
(3)设 =x
=x ,则
,则
 ,
,
=
=|x-1|+2|x-2|+3|x-3|+…+9|x-9|+10|x-10|
当x∈[k,k+1]时,k∈{0,1,2,3,4,5,6,7,8,9}
f(x)=(x-1)+2(x-2)+…+k(x-k)+k(k+1-x)…+10(10-x)
=x+2x+…+kx-(k+1)x-(k+2)x-…-10x-12-22-…-k2+(k+1)2+(k+2)2+…+102
=(k2+k-55)x-[12+22+…+k2-(k+1)2-(k+2)2-…-102]
当k∈{0,1,2,3,4,5,6}时,k2+k-55<0,函数为减函数
当k∈{7,8,9}时,k2+k-55>0,函数为增函数
故当k=7时,f(P)取最小值f(7)=1×6+2×5+3×4+4×3+5×2+6×1+7×0+8×1+9×2+10×3=112
点评:本题考查的知识点是平面向量加法和减法的三角形法则,向量定比分点公式,含绝对值符号的函数,是平面向量的综合应用,难度较大,属于难题.
 =
= -
- ,再由
,再由 ,
, =
= +
+ 可得答案;
可得答案;(2)根据向量定比分点公式,当C将AB分为长度比为a:b的两段时,
 =
= ,逐一求出各分点对应的向量累加可得答案.
,逐一求出各分点对应的向量累加可得答案.(3)设
 =x
=x ,则
,则 =|x-1|+2|x-2|+3|x-3|+…+9|x-9|+10|x-10|利用零点分段法化简函数的解析式,并结合一次函数的图象和性质分析函数的单调性,可得函数的最小值.
=|x-1|+2|x-2|+3|x-3|+…+9|x-9|+10|x-10|利用零点分段法化简函数的解析式,并结合一次函数的图象和性质分析函数的单调性,可得函数的最小值.解答:解:(1)在△OAB中
 =
= -
-
∴
 =t
=t -t
-t
∴
 =
= +
+ =t
=t +(1-t)
+(1-t)
(2)∵C1、C2,…,C9依次为线段AB的10等分点,
∴
 =
=
 +
+
 ;
; =
=
 +
+
 ;
;…
 =
=
 +
+
 ;
;…
 =
=
 +
+
 ;
;∴
 =(
=( +
+ +…+
+…+ )
) =
=

故λ=

(3)设
 =x
=x ,则
,则 ,
,=

=|x-1|+2|x-2|+3|x-3|+…+9|x-9|+10|x-10|
当x∈[k,k+1]时,k∈{0,1,2,3,4,5,6,7,8,9}
f(x)=(x-1)+2(x-2)+…+k(x-k)+k(k+1-x)…+10(10-x)
=x+2x+…+kx-(k+1)x-(k+2)x-…-10x-12-22-…-k2+(k+1)2+(k+2)2+…+102
=(k2+k-55)x-[12+22+…+k2-(k+1)2-(k+2)2-…-102]
当k∈{0,1,2,3,4,5,6}时,k2+k-55<0,函数为减函数
当k∈{7,8,9}时,k2+k-55>0,函数为增函数
故当k=7时,f(P)取最小值f(7)=1×6+2×5+3×4+4×3+5×2+6×1+7×0+8×1+9×2+10×3=112
点评:本题考查的知识点是平面向量加法和减法的三角形法则,向量定比分点公式,含绝对值符号的函数,是平面向量的综合应用,难度较大,属于难题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
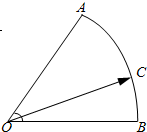 (2013•杭州一模)如图,在扇形OAB中,∠AOB=60°,点C为弧AB上的一个动点.若
(2013•杭州一模)如图,在扇形OAB中,∠AOB=60°,点C为弧AB上的一个动点.若 ,求证:
,求证: ;
; ,
, ,且C为线段AB上靠近A的一个三等分点,求
,且C为线段AB上靠近A的一个三等分点,求 的值;
的值; ,
, ,且P1,P2,P3,…,Pn-1为线段AB的n(n≥2)个等分点,求
,且P1,P2,P3,…,Pn-1为线段AB的n(n≥2)个等分点,求 的值.
的值.