Question

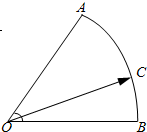（2013•杭州一模）如图，在扇形OAB中，∠AOB=60°，点C为弧AB上的一个动点．若

OC

=x

OA

+y

OB

，则x+3y的取值范围是

[1，3]

．

Answer 1

分析：过点C作CE∥OB，交OA于E，再作CF∥OA，交OB于F．平行四边形OECF中，可得

OC

=

OE

+

OF

，结合平面向量基本定理得到

OE

=x

OA

，

OF

=y

OB

．考虑到x、y均为正数且x+3y中y的系数较大，所以当y越大时x+3y的值越大，因此将点C沿AB弧由A向B运动，加以观察即可得到x+3y的取值范围．

解答：解：过点C作CE∥OB，交OA于E，再作CF∥OA，交OB于F，可得
∵四边形OECF是平行四边形
∴

OC

=

OE

+

OF

∵

OC

=x

OA

+y

OB

，

OE

与

OA

是共线向量且

OF

与

OB

是共线向量，
∴

OE

=x

OA

，

OF

=y

OB

根据

OE

与

OA

同向、

OF

与

OB

同向，可得x=

|OE|

|OA|

且y=

|OF|

|OB|

∵x、y均为正数且x+3y中y的系数较大，当点C沿AB弧由A向B运动的过程中，
|

OE

|变短而|

OF

|变长
∴当C与A重合时，x=1达到最大而y=0达到最小，此时x+3y有最小值为1；
当C与A重合时，x=0达到最小而y=1达到最大，此时x+3y有最大值为3
即x+3y的取值范围是[1，3]
故答案为：[1，3]

点评：本题给出扇形OAB的弧AB上动点C，在

OC

=x

OA

+y

OB

的情况下求x+3y的取值范围．着重考查了平面向量基本定理、向量的线性运算法则和二元函数最值求法等知识，属于中档题．