题目内容
已知 =
= ,
, =
= ,若存在非零实数k,t使得
,若存在非零实数k,t使得 ,
, ,且
,且 ⊥
⊥ ,试求:
,试求: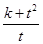 的最小值.
的最小值.
 .
.
解析试题分析:根据题意 =
= ,
, =
= ,可得
,可得 ,又∵
,又∵ ⊥
⊥ ,∴
,∴ ,将
,将 ,
, 代入化简后得
代入化简后得 ,
,
因此 ,这是一个关于t的二次函数,利用二次函数求最值的相关方法,可以得到
,这是一个关于t的二次函数,利用二次函数求最值的相关方法,可以得到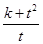 的最小值为
的最小值为 .
.
∵ =
= ,
, =
= ,∴
,∴ ,
,
又∵ ⊥
⊥ ,∴
,∴ 3分,
3分,
化简得 5分,
5分,
∴ 8分,
8分,
∴当t=-2时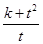 有最小值
有最小值 10分.
10分.
考点:1、平面向量的数量积;2、二次函数求最值.

练习册系列答案
相关题目
 中,
中, ,
, ,设
,设 .
. 时,求
时,求 的值;
的值; ,求
,求 的值.
的值. ,
, ,且
,且 .
. 的轨迹
的轨迹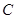 的方程;
的方程; 相交于不同的两点
相交于不同的两点 ,又点
,又点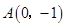 ,当
,当 时,求实数
时,求实数 的取值范围.
的取值范围. 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中
 ,且
,且 ,求:
,求: 的坐标;
的坐标;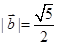 ,且
,且 与
与 垂直,求
垂直,求 与
与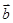 的夹角;
的夹角;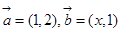
 为锐角,求
为锐角,求 的范围;
的范围;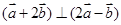 时,求
时,求 为坐标原点,
为坐标原点, .
. 的大小(结果用反三角函数值表示);
的大小(结果用反三角函数值表示); 为
为 轴上一点,求
轴上一点,求 的最大值及取得最大值时点
的最大值及取得最大值时点 、
、 不共线
不共线 ,求证:A、B、D三点共线;
,求证:A、B、D三点共线; 和
和 共线.
共线. 与
与 的夹角为120°,且
的夹角为120°,且 ,则
,则 ______________
______________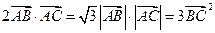 ,求角A、B、C的大小.
,求角A、B、C的大小.