题目内容
在 中,
中, ,
, ,设
,设 .
.
(1)当 时,求
时,求 的值;
的值;
(2)若 ,求
,求 的值.
的值.
(1)-36; (2) .
.
解析试题分析:(1)画出图形:  取
取 为基底,则向量
为基底,则向量 就可用
就可用 两向量表示出来,再由已知能计算出
两向量表示出来,再由已知能计算出 的值;另也可以选取A为原点,AB为x轴,建立平面直角,从而用向量的坐标来加以解决;从标法学生也较易掌握;(2)同(1)将向量
的值;另也可以选取A为原点,AB为x轴,建立平面直角,从而用向量的坐标来加以解决;从标法学生也较易掌握;(2)同(1)将向量 就可用
就可用 两向量表示出来,只是不要将
两向量表示出来,只是不要将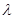 换成2;则
换成2;则 就可化为关于
就可化为关于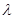 方程,解此方程即得结果.也可用坐标法进行解决.
方程,解此方程即得结果.也可用坐标法进行解决.
试题解析:(1)当 时,
时, ,
,
所以 , 3分
, 3分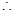
 . 7分
. 7分
(2)因为
 , 12分
, 12分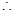
 ,解得
,解得 . 14分
. 14分
(说明:利用其它方法解决的,类似给分)
考点:1.向量的加减法;2.向量的数量积.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
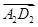 -
-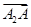 )-
)-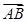 ;②(
;②(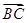 +
+ )-
)-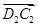 ;③(
;③(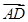 -
-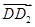 ;④(
;④(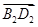 +
+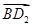 的是________
的是________  =(1,2),
=(1,2), =(-2,n) (n>1),
=(-2,n) (n>1), 与
与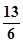 ,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+
,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+ )的值.
)的值. ·
· =
=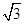 |
| |2,求角A,B,C的大小.
|2,求角A,B,C的大小. 、
、 、
、 、
、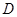 的坐标分别为
的坐标分别为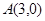 、
、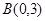 、
、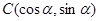 、
、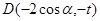 ,
,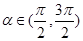
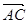 |=|
|=|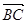 |,求角
|,求角 的值;
的值; ,求
,求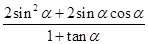 的值.
的值.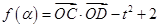 在定义域
在定义域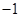 ,求
,求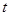 的值.
的值. =
= ,
, =
= ,若存在非零实数k,t使得
,若存在非零实数k,t使得 ,
, ,且
,且 ⊥
⊥ ,试求:
,试求: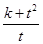 的最小值.
的最小值. 中,O为坐标原点,已知点A
中,O为坐标原点,已知点A
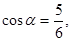 求证:
求证: ;
; 求
求 的值.
的值. 是非零向量)
是非零向量) ,则
,则 ;
; ,则
,则 ;
;