题目内容
设两个非零向量 、
、 不共线
不共线
(1)若 ,求证:A、B、D三点共线;
,求证:A、B、D三点共线;
(2)试确定实数k的值,使 和
和 共线.
共线.
(1) 先证明 共线;(2)k=±1
共线;(2)k=±1
解析试题分析:(1)因为, ,
,
所以, ,即
,即 共线,又它们有公共点,所以,A、B、D三点共线。
共线,又它们有公共点,所以,A、B、D三点共线。
(2)因为, 和
和 共线.所以,存在唯一实数
共线.所以,存在唯一实数 ,使
,使 =
= (
( ),
),
即 ,解得,k=±1。
,解得,k=±1。
考点:平面向量的线性运算,平面向量的数量积,平面向量的应用。
点评:典型题,证明三点共线,一般方法是,证明三点所确定的两向量共线,利用它们有公共点,达到证明目的。根据两向量共线,求参数问题,一般方法是,利用共线向量定理,建立参数的方程组。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 =
= ,
, =
= ,若存在非零实数k,t使得
,若存在非零实数k,t使得 ,
, ,且
,且 ⊥
⊥ ,试求:
,试求: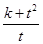 的最小值.
的最小值. 中,O为坐标原点,已知点A
中,O为坐标原点,已知点A
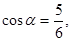 求证:
求证: ;
; 求
求 的值.
的值. 与
与 共线,设函数
共线,设函数 .
. 的周期及最大值;
的周期及最大值; ,边 BC=
,边 BC= ,
, ,求 △ABC 的面积.
,求 △ABC 的面积. 的内角,
的内角, 分别是其对边长,向量
分别是其对边长,向量 ,
, ,
, .
.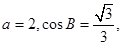 求
求 的长.
的长. 
 的值;
的值; 且
且 ,求
,求 。
。 ,
, 。
。 及
及 ;
; 的最小值是
的最小值是 ,求
,求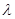 的值。
的值。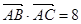 ,记
,记 ,△ABC的面积为
,△ABC的面积为 ,且满足
,且满足 .
. 的取值范围;
的取值范围; 的最大值和最小值.
的最大值和最小值. ,
, ,求x,y的值使
,求x,y的值使 ,且
,且 。
。