题目内容
8.在△ABC中,若$\overrightarrow{AB}•\overrightarrow{BC}=-2,|{\overrightarrow{BA}-\overrightarrow{BC}}|=\sqrt{2}$,则△ABC的面积的最大值为( )| A. | 5 | B. | 3 | C. | $\frac{5}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
分析 根据△ABC中$\overrightarrow{AB}$•$\overrightarrow{BC}$=-2,得ca•cosB=2①;
由|$\overrightarrow{BA}$-$\overrightarrow{BC}$|=$\sqrt{2}$得b=$\sqrt{2}$,再由余弦定理得出c2+a2的值;
根据同角的三角函数关系和基本不等式即可求出S△ABC的最大值.
解答 解:△ABC中,A、B、C所对边分别为a,b,c,
由$\overrightarrow{AB}$•$\overrightarrow{BC}$=-2,得ca•cos(π-B)=-2,
∴ca•cosB=2①;
由|$\overrightarrow{BA}$-$\overrightarrow{BC}$|=$\sqrt{2}$,得b=$\sqrt{2}$,
∴b2=c2+a2-2ca•cosB=2②;
∴c2+a2=6,
∴S△ABC=$\frac{1}{2}$acsinB
=$\frac{1}{2}$ac$\sqrt{1{-cos}^{2}B}$
=$\frac{1}{2}$ac$\sqrt{1-\frac{4}{{(ac)}^{2}}}$
=$\frac{1}{2}$$\sqrt{{(ac)}^{2}-4}$;
由a2+c2=6,得a2+c2≥2ac,ac≤3,当且仅当a=c=$\sqrt{3}$时取等号,
所以S△ABC≤$\frac{1}{2}$$\sqrt{{3}^{2}-4}$=$\frac{\sqrt{5}}{2}$,
即△ABC面积的最大值为$\frac{\sqrt{5}}{2}$.
故选:D.
点评 本题考查平面向量数量积的运算、三角形面积公式不等式求最值等知识,是综合性题目.

练习册系列答案
相关题目
18.二次不等式-$\frac{a}{3}$x2+2bx-c<0的解集是全体实数的充要条件是( )
| A. | $\left\{\begin{array}{l}{a>0}\\{4{b}^{2}-\frac{4}{3}ac<0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a>0}\\{4{b}^{2}-\frac{4}{3}ac>0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a<0}\\{4{b}^{2}-\frac{4}{3}ac>0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a<0}\\{4{b}^{2}-\frac{4}{3}ac<0}\end{array}\right.$ |
3.已知集合A={x|log2(x+1)>0},B={x|0<x<1},则∁AB=( )
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
17.在空间四面体EFGH中,点I是面FGH的重心,则$\overrightarrow{EI}$=( )
| A. | $\frac{1}{2}$$\overrightarrow{EF}$+$\frac{1}{2}$$\overrightarrow{EG}$+$\frac{1}{2}$$\overrightarrow{EH}$ | B. | $\frac{1}{5}$$\overrightarrow{EF}$+$\frac{1}{5}$$\overrightarrow{EG}$+$\frac{1}{5}$$\overrightarrow{EH}$ | C. | $\frac{1}{4}$$\overrightarrow{EF}$+$\frac{1}{4}$$\overrightarrow{EG}$+$\frac{1}{4}$$\overrightarrow{EH}$ | D. | $\frac{1}{3}$$\overrightarrow{EF}$+$\frac{1}{3}$$\overrightarrow{EG}$+$\frac{1}{3}$$\overrightarrow{EH}$ |
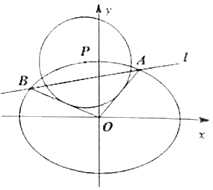 如图,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{3}}}{2}$,P为椭圆E上的动点,P到点M(0,2)的距离的最大值为$\frac{2}{3}\sqrt{21}$,直线l交椭圆于A(x1,y1)、B(x2,y2)两点.
如图,已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$e=\frac{{\sqrt{3}}}{2}$,P为椭圆E上的动点,P到点M(0,2)的距离的最大值为$\frac{2}{3}\sqrt{21}$,直线l交椭圆于A(x1,y1)、B(x2,y2)两点.