题目内容
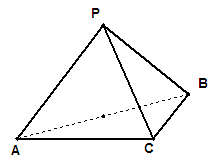
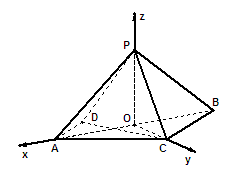
(本题满分12分)三棱锥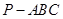 中,
中,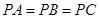 ,
,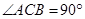 ,
,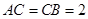 .
.
(Ⅰ)求证:平面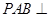 平面
平面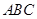 ;
;
(Ⅱ)若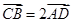 ,且异面直线
,且异面直线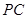 与
与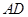 的夹角为
的夹角为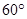 时,求二面角
时,求二面角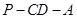 的余弦值.
的余弦值.
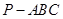 中,
中,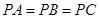 ,
,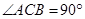 ,
,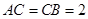 .
. 
(Ⅰ)求证:平面
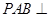 平面
平面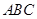 ;
;(Ⅱ)若
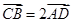 ,且异面直线
,且异面直线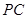 与
与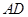 的夹角为
的夹角为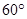 时,求二面角
时,求二面角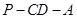 的余弦值.
的余弦值.(1)通过建立空间直角坐标系来分析,或者利用线面垂直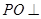 平面
平面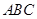 ,进而得到面面垂直。
,进而得到面面垂直。
(2)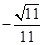
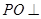 平面
平面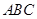 ,进而得到面面垂直。
,进而得到面面垂直。(2)
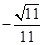
试题分析:证明:(Ⅰ)作
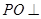 平面
平面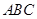 于点
于点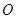 ,∵
,∵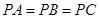 ,
,
∴
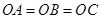 ,即
,即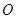 为
为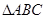 的外心
的外心又∵
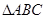 中,
中,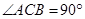
故
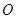 为
为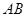 边的中点
边的中点所以
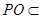 平面
平面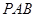
即证:平面
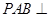 平面
平面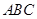 . .......6分
. .......6分(Ⅱ)∵
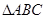 中,
中,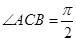 ,
,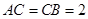 ,∴
,∴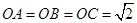
∵
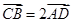 ,且异面直线
,且异面直线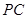 与
与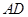 的夹角为
的夹角为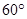 ,
,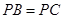
∴
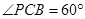 ,∴
,∴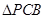 为正三角形,可解得
为正三角形,可解得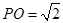 .
.以
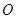 为坐标原点,建立如图所示空间直角坐标系
为坐标原点,建立如图所示空间直角坐标系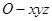 ,则
,则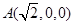 ,
, 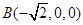 ,
,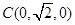 ,
,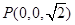
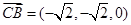
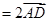 ,∴
,∴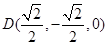 . …………………….9分
. …………………….9分设平面
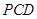 的法向量为
的法向量为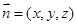
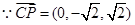 ,
,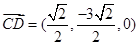
由
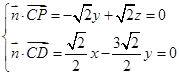 , 取
, 取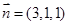
平面
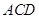 的法向量为
的法向量为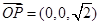
∴
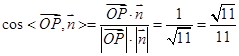 .
.由图可知,所求二面角
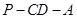 为钝角,其的余弦值为
为钝角,其的余弦值为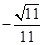 . ……….12分
. ……….12分点评:解决该类立体几何问题,尤其是二面角的求解,通常情况下,都是建立空间直角坐标系,借助于法向量来求解二面角的方法。而对于面面垂直的证明,一般都是利用线面垂直为前提,结合面面垂直的判定定理得到,属于中档题。

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
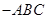 中
中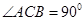 ,
,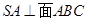 ,
,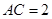 ,
,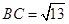 ,
,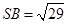 .
.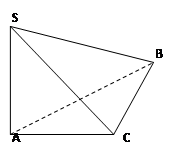
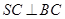 。
。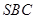 与底面
与底面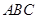 所成二面角的大小。
所成二面角的大小。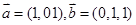 那么这条斜线与平面所成的角是 ____________
那么这条斜线与平面所成的角是 ____________ 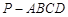 的底面
的底面 为菱形,
为菱形,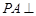 平面
平面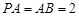 , E、F分别为
, E、F分别为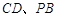 的中点,
的中点,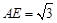 .
.
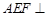 平面
平面 .
. 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.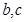 表示两条直线,
表示两条直线,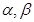 表示两个平面,则下列命题是真命题的是( )
表示两个平面,则下列命题是真命题的是( ) ,
, ∥
∥ ,则
,则

 ,则
,则

 的长轴为
的长轴为
 ,短轴为
,短轴为
 ,将椭圆沿y轴折成一个二面角,使得
,将椭圆沿y轴折成一个二面角,使得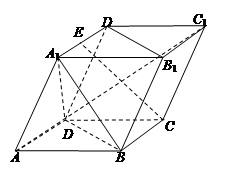
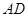 与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④
与CC1所成的角;②三棱锥A1-ABD是正三棱锥;③CE⊥平面BB1D1D;④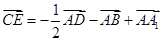 ;⑤|
;⑤|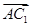 |=
|=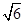 .其中正确的命题有_____________.(写出所有正确命题的序号)
.其中正确的命题有_____________.(写出所有正确命题的序号)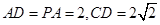 ,E、F分别是AB、PD的中点.
,E、F分别是AB、PD的中点.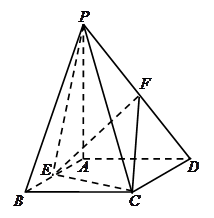
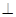 平面PCD;
平面PCD;