题目内容
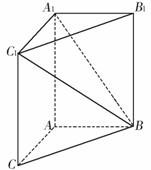
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(Ⅰ)求直线B1C1与平面A1BC1所成角的正弦值;
(Ⅱ)在线段BC1上确定一点D,使得AD⊥A1B,并求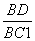 的值.
的值.
解:(Ⅰ)∵AA1C1C为正方形,∴AA1⊥AC.
∵平面ABC⊥平面AA1C1C,
∴AA1⊥平面ABC,
∴AA1⊥AC,AA1⊥AB.
由已知AB=3,BC=5,AC=4,∴AB⊥AC.
如图,以A为原点建立空间直角坐标系A-xyz,则B(0,3,0),A1(0,0,4),B1(0,3,4),C1(4,0,4),
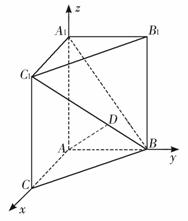 ∴
∴ =(0,3,-4),
=(0,3,-4),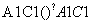 =(4,0,0),
=(4,0,0),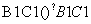 =(4,-3,0).
=(4,-3,0).
设平面A1BC1的法向量为n=(x,y,z),则
 即
即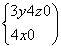
令z=3,则x=0,y=4,∴n=(0,4,3).
设直线B1C1与平面A1BC1所成的角为θ,则
sinθ=|cos<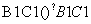 ,n>|=
,n>|=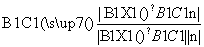 =
=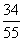 =
=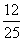 .
.
故直线B1C1与平面A1BC1所成角的正弦值为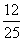 .
.
(Ⅱ)设D(x,y,z)是线段BC1上一点,且 =λ
=λ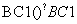 (λ∈[0,1]),
(λ∈[0,1]),
∴(x,y-3,z)=λ(4,-3,4),
∴x=4λ,y=3-3λ,z=4λ,
∴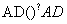 =(4λ,3-3λ,4λ).
=(4λ,3-3λ,4λ).
又 =(0,3,-4),
=(0,3,-4),
由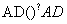 ·
· =0,得3(3-3λ)-4×4λ=0,
=0,得3(3-3λ)-4×4λ=0,
即9-25λ=0,解得λ=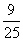 ∈[0,1].
∈[0,1].
故在线段BC1上存在点D,使得AD⊥A1B.
此时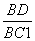 =λ=
=λ=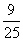 .
.

练习册系列答案
相关题目
 与曲线
与曲线 恰有两个不同的的交点,则
恰有两个不同的的交点,则 ____________.
____________. 的焦点坐标是_____________ 。
的焦点坐标是_____________ 。 +b
+b =1”是“a2+b2=1”的
=1”是“a2+b2=1”的 sin2x+2cos2x+m在区间[0,
sin2x+2cos2x+m在区间[0, ]上的最大值为3,则
]上的最大值为3,则 ,则实数a的值是( )
,则实数a的值是( ) B.
B. C.
C. D.-
D.- 的定义域为
的定义域为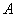 ,若存在非零实数
,若存在非零实数 ,使得对于任意
,使得对于任意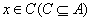 有
有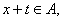 且
且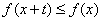 ,则称
,则称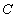 上的
上的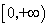 的函数
的函数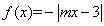 ,且
,且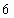 度低调函数,那么实数
度低调函数,那么实数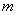 的取值范围是( )
的取值范围是( )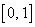 B.
B. 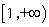
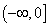 D.
D.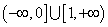
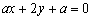 和直线
和直线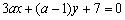 平行,则
平行,则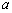 的值为 .
的值为 . 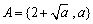 ,
,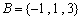 ,且
,且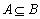 ,则实数
,则实数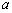 的值是 .
的值是 .