题目内容
(本小题满分12分)
已知点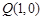 在椭圆C:
在椭圆C: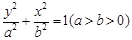 上,且椭圆C的离心率
上,且椭圆C的离心率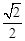 .
.
(Ⅰ)求椭圆C的方程;
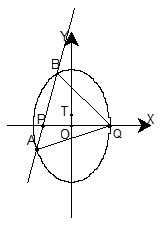
(Ⅱ)过点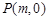 作直线交椭圆C于点A.B.△ABQ的垂心为T,是否存在实数m ,使得垂心T在y轴上.若存在,求出实数m的取值范围;若不存在,请说明理由.
作直线交椭圆C于点A.B.△ABQ的垂心为T,是否存在实数m ,使得垂心T在y轴上.若存在,求出实数m的取值范围;若不存在,请说明理由.
已知点
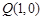 在椭圆C:
在椭圆C: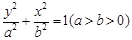 上,且椭圆C的离心率
上,且椭圆C的离心率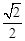 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点
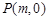 作直线交椭圆C于点A.B.△ABQ的垂心为T,是否存在实数m ,使得垂心T在y轴上.若存在,求出实数m的取值范围;若不存在,请说明理由.
作直线交椭圆C于点A.B.△ABQ的垂心为T,是否存在实数m ,使得垂心T在y轴上.若存在,求出实数m的取值范围;若不存在,请说明理由.(Ⅰ) 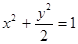 (Ⅱ)
(Ⅱ)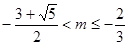
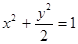 (Ⅱ)
(Ⅱ)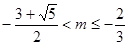
试题分析:(Ⅰ)
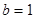 ,
,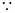
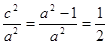 ,
,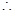
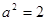
 椭圆C的方程为
椭圆C的方程为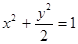 ——————————————2分
——————————————2分(Ⅱ)假设存在实数m,使得垂心T在Y轴上。
当直线斜率不存在时,设
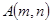 ,则
,则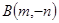 则有
则有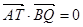 ,所以
,所以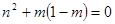
又
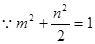 可解得
可解得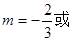
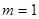 (舍)
(舍) 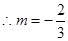 ——————4分
——————4分当直线斜率存在时,设
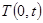 (
(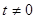 )
)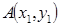 ,
,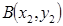
设直线方程为:
 则
则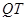 斜率为
斜率为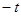 ,
,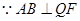 ,
,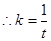
又
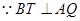 ,
,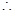
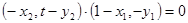
即:

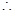
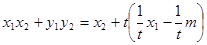
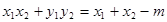 ————————————6分
————————————6分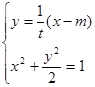 消去
消去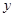 可得:
可得: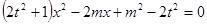
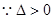
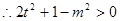
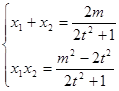
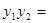
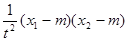 =
=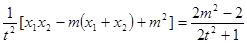 ——————8分
——————8分代入可得(
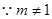 )
)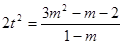
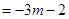
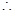
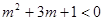
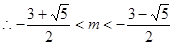 --10分
--10分又
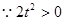
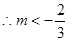
综上知实数m的取值范围
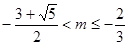 ——————————12分
——————————12分点评:对于直线与圆锥曲线的综合问题,往往要联立方程,同时结合一元二次方程根与系数的关系进行求解;而对于最值问题,则可将该表达式用直线斜率k表示,然后根据题意将其进行化简结合表达式的形式选取最值的计算方式

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的方程为
的方程为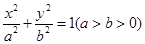 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).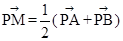 ,求点
,求点 的坐标;
的坐标;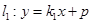 交椭圆
交椭圆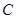 、
、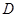 两点,交直线
两点,交直线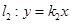 于点
于点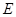 .若
.若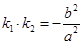 ,证明:
,证明: 的中点;
的中点; 、
、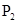 满足
满足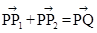 ,写出求作点
,写出求作点 )与抛物线
)与抛物线 =2x上的点P的距离为
=2x上的点P的距离为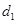 ,P到抛物线准线l的距为
,P到抛物线准线l的距为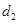 ,则
,则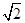 )
)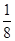 ,-
,-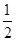 )
)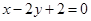 经过椭圆
经过椭圆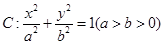 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆 的右顶点为
的右顶点为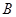 ,点
,点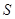 和椭圆
和椭圆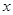 轴上方的动点,直线,
轴上方的动点,直线,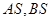 与直线
与直线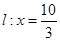 分别交于
分别交于 两点。
两点。
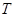 ,使得
,使得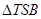 的面积为
的面积为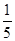 ?若存在,确定点
?若存在,确定点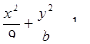 的右焦点F2重合,F1是椭圆的左焦点;
的右焦点F2重合,F1是椭圆的左焦点;  ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求
ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求 ,∠PF2F1=
,∠PF2F1= ,求cos
,求cos 的值及
的值及 上点
上点 处的切线平行于直线
处的切线平行于直线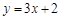 ,那么点
,那么点
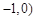
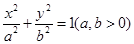 的焦点坐标为
的焦点坐标为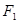 (
(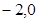 ),点M(
),点M(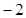 ,
,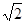 )在椭圆E上.
)在椭圆E上.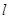 与椭圆E交于
与椭圆E交于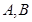 两点,求线段
两点,求线段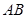 中点
中点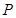 的轨迹方程;
的轨迹方程;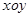 中,点
中,点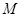 到两定点F1
到两定点F1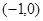 和F2
和F2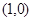 的距离之和为
的距离之和为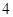 ,设点
,设点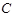 .(1)求曲线
.(1)求曲线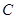 的方程; (2)若直线
的方程; (2)若直线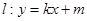 与曲线
与曲线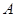 、
、 (
(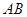 为直径的圆过点
为直径的圆过点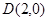 ,试判断直线
,试判断直线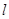 是否经过一定点,若是,求出定点坐标;若不是,说明理由.
是否经过一定点,若是,求出定点坐标;若不是,说明理由. 为椭圆
为椭圆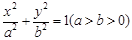 上的一个动点,弦
上的一个动点,弦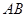 、
、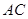 分别过焦点
分别过焦点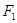 、
、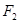 ,当
,当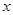 轴时,恰好有
轴时,恰好有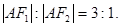
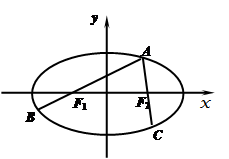
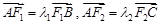 .
.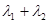 的值;
的值;