题目内容
(本小题满分12分)
已知抛物线C1:y2=4x的焦点与椭圆C2: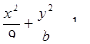 的右焦点F2重合,F1是椭圆的左焦点;
的右焦点F2重合,F1是椭圆的左焦点;
(Ⅰ)在 ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求
ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求 ABC重心G的轨迹方程;
ABC重心G的轨迹方程;
(Ⅱ)若P是抛物线C1与椭圆C2的一个公共点,且∠PF1F2=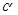 ,∠PF2F1=
,∠PF2F1=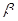 ,求cos
,求cos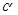
 的值及
的值及 PF1F2的面积。
PF1F2的面积。
已知抛物线C1:y2=4x的焦点与椭圆C2:
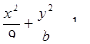 的右焦点F2重合,F1是椭圆的左焦点;
的右焦点F2重合,F1是椭圆的左焦点; (Ⅰ)在
 ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求
ABC中,若A(-4,0),B(0,-3),点C在抛物线y2=4x上运动,求 ABC重心G的轨迹方程;
ABC重心G的轨迹方程;(Ⅱ)若P是抛物线C1与椭圆C2的一个公共点,且∠PF1F2=
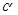 ,∠PF2F1=
,∠PF2F1=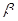 ,求cos
,求cos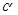
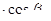 的值及
的值及 PF1F2的面积。
PF1F2的面积。(Ⅰ) (y+1)2= .(Ⅱ)
.(Ⅱ)  .
.
 .(Ⅱ)
.(Ⅱ)  .
.试题分析:(Ⅰ)设重心G(x,y),则
 整理得
整理得 ………2分
………2分将(*)式代入y2=4x中,得(y+1)2=
 ∴
∴ 重心G的轨迹方程为(y+1)2=
重心G的轨迹方程为(y+1)2= .………4分
.………4分(Ⅱ) ∵椭圆与抛物线有共同的焦点,由y2=4x得F2(1,0),∴b2=8,椭圆方程为
 .………6分
.………6分设P(x1,y1) 由
 得
得 ,∴x1=
,∴x1= ,x1=-6(舍).
,x1=-6(舍).∵x=-1是y2=4x的准线,即抛物线的准线过椭圆的另一个焦点F1。
设点P到抛物线y2=4x的准线的距离为PN,则︱PF2︱=︱PN︱.
又︱PN︱=x1+1=
 ,
,∴
 .………………………8分
.………………………8分过点P作PP1⊥x轴,垂足为P1,在Rt△PP1F1中,cosα=
 在Rt△PP1F2中,cos(л-β)=
在Rt△PP1F2中,cos(л-β)= ,cosβ=
,cosβ= ,∴cosαcosβ=
,∴cosαcosβ= 。………………………………10分
。………………………………10分∵x1=
 ,∴∣PP1∣=
,∴∣PP1∣= ,∴
,∴ .………………………12分
.………………………12分点评:此类问题利用动点是定曲线上的动点,另一动点依赖于它,那么可寻求它们坐标之间的关系,然后代入定曲线的方程进行求解,就得到原动点的轨迹

练习册系列答案
相关题目
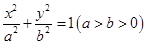 的离心率
的离心率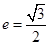 ,且短半轴
,且短半轴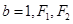 为其左右焦点,
为其左右焦点,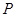 是椭圆上动点.
是椭圆上动点.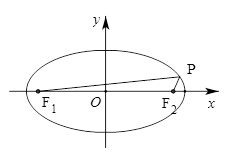
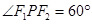 时,求
时,求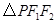 面积;
面积;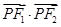 取值范围.
取值范围.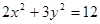 的两焦点之间的距离为
的两焦点之间的距离为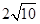
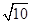
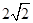
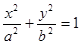 (
(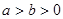 ),点
),点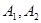 为椭圆C的左、右顶点。
为椭圆C的左、右顶点。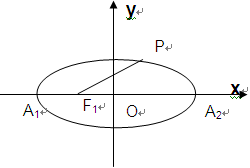
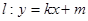 与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足
与(1)中所述椭圆C相交于A、B两点(A、B不是左、右顶点),且满足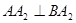 ,求证:直线
,求证:直线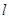 过定点,并求出该点的坐标。
过定点,并求出该点的坐标。 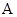 、
、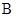 、
、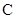 是椭圆
是椭圆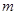 :
: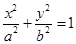 (
(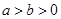 )上的三点,其中点
)上的三点,其中点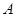 的坐标为
的坐标为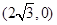 ,
,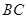 过椭圆的中心,且
过椭圆的中心,且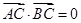 ,
,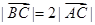 。
。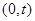 的直线
的直线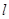 (斜率存在时)与椭圆
(斜率存在时)与椭圆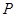 ,
,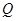 ,设
,设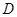 为椭圆
为椭圆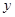 轴负半轴的交点,且
轴负半轴的交点,且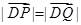 ,求实数
,求实数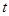 的取值范围.
的取值范围.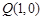 在椭圆C:
在椭圆C: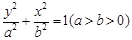 上,且椭圆C的离心率
上,且椭圆C的离心率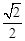 .
.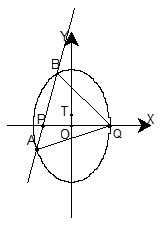
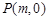 作直线交椭圆C于点A.B.△ABQ的垂心为T,是否存在实数m ,使得垂心T在y轴上.若存在,求出实数m的取值范围;若不存在,请说明理由.
作直线交椭圆C于点A.B.△ABQ的垂心为T,是否存在实数m ,使得垂心T在y轴上.若存在,求出实数m的取值范围;若不存在,请说明理由.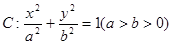 长轴的一个顶点作圆
长轴的一个顶点作圆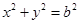 的两条切线,切点分别为
的两条切线,切点分别为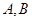 ,若
,若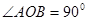 (
(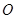 是坐标原点),则椭圆
是坐标原点),则椭圆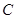 的离心率为_________.
的离心率为_________.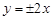 的是
的是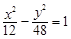
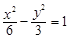
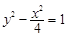
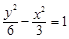
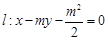 ,椭圆C:
,椭圆C: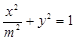 ,
,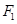 、
、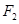 分别为椭圆C的左、右焦点.
分别为椭圆C的左、右焦点.