题目内容
【题目】![]() 公司从某大学招收毕业生,经过综合测试,录用了
公司从某大学招收毕业生,经过综合测试,录用了![]() 名男生和
名男生和![]() 名女生,这
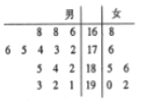
名女生,这![]() 名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在
名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在![]() 分以上者到甲部门工作;
分以上者到甲部门工作;![]() 分以下者到乙部门工作,另外只有成绩高于
分以下者到乙部门工作,另外只有成绩高于![]() 分才能担任助理工作。
分才能担任助理工作。
(1)如果用分层抽样的方法从甲部门人选和乙部门人选中选取![]() 人,再从这
人,再从这![]() 人中选
人中选![]() 人,那么至少有一人是甲部门人选的概率是多少?
人,那么至少有一人是甲部门人选的概率是多少?
(2)若从所有甲部门人选中随机选![]() 人,用
人,用![]() 表示所选人员中能担任助理工作的男生人数,写出
表示所选人员中能担任助理工作的男生人数,写出![]() 的分布列,并求出
的分布列,并求出![]() 的数学期望.
的数学期望.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
试题分析:(1)根据分层抽样和茎叶图可知甲乙两部门选中的人数均为![]() 人,要求“至少有一人是甲部门人选的概率”,可求其对立事件“选中的
人,要求“至少有一人是甲部门人选的概率”,可求其对立事件“选中的![]() 人都是乙部门”的概率即可;(2)设选毕业生中能担任助理工作的男生人数
人都是乙部门”的概率即可;(2)设选毕业生中能担任助理工作的男生人数![]() ,其可能的取值分别为
,其可能的取值分别为![]() ,根据超几何分布求出
,根据超几何分布求出![]() 取各值的概率,得其分布列和期望.
取各值的概率,得其分布列和期望.
试题解析:(1)用分层抽样的方法,每个人被抽中的概率为![]() ,根据茎叶图,有甲部门人选
,根据茎叶图,有甲部门人选![]() 人,乙部门人选
人,乙部门人选![]() 人,所以选中的甲部门人选有
人,所以选中的甲部门人选有![]() (人),乙部门人选有
(人),乙部门人选有![]() (人),用事件
(人),用事件![]() 表示“至少有一名甲部门人被选中”,则它的对立事件
表示“至少有一名甲部门人被选中”,则它的对立事件![]() 表示“没有一名甲部门人被选中”,则
表示“没有一名甲部门人被选中”,则![]() ,因此至少有一人是甲部门人选的概率是
,因此至少有一人是甲部门人选的概率是![]() .
.
(2)依据题意,所选毕业生中能担任助理工作的男生人数![]() 的取值分别为
的取值分别为![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因此![]() 的分布列如下:
的分布列如下:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
数学期望![]() .
.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】某中学有一调查小组为了解本校学生假期中白天在家时间的情况,从全校学生中抽取![]() 人,统计他们平均每天在家的时间(在家时间在
人,统计他们平均每天在家的时间(在家时间在![]() 小时以上的就认为具有“宅”属性,否则就认为不具有“宅”属性)
小时以上的就认为具有“宅”属性,否则就认为不具有“宅”属性)
具有“宅”属性 | 不具有“宅”属性 | 总计 | |
男生 | 20 | 50 | 70 |
女生 | 10 | 40 | 50 |
总计 | 30 | 90 | 120 |
(1)请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断能否在犯错误的概率不超过
列联表,并通过计算判断能否在犯错误的概率不超过
![]() 的前提下认为“是否具有‘宅’属性与性别有关?”
的前提下认为“是否具有‘宅’属性与性别有关?”
(2)采用分层抽样的方法从具有“宅”属性的学生里抽取一个![]() 人的样本,其中男生和女生各多少人?
人的样本,其中男生和女生各多少人?
从![]() 人中随机选取
人中随机选取![]() 人做进一步的调查,求选取的
人做进一步的调查,求选取的![]() 人至少有
人至少有![]() 名女生的概率.
名女生的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 5.635 | 7.879 | 10.828 |