题目内容
4.设Sn是等差数列{an}的前n项和,a1=2,a5=3a3,则a3=( )| A. | -2 | B. | 0 | C. | 3 | D. | 6 |
分析 利用等差数列的通项公式即可求得公差d,再利用等差数列的通项公式即可求出答案.
解答 解:设等差数列{an}的公差为d,
∵a1=2,a5=3a3,∴2+4d=3(2+2d),解得d=-2.
则a3=a1+2d=2+2×(-2)=-2.
故选:A.
点评 本题考查等差数列的通项公式,求出数列的公差是解决问题的关键,属基础题.

练习册系列答案
相关题目
15.sin(-1740°)的值是( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
16.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )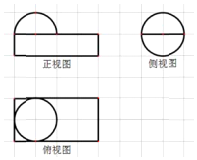

| A. | $\frac{14π}{3}$ | B. | $\frac{10π}{3}$ | C. | $\frac{8π}{3}$ | D. | $\frac{5π}{3}$ |
13.已知集合A={x|2x-1<0},B={x|0≤x≤1},那么A∩B等于( )
| A. | {x|x≥0} | B. | {x|x≤1} | C. | {x|0<x<$\frac{1}{2}$} | D. | {x|0≤x<$\frac{1}{2}$} |
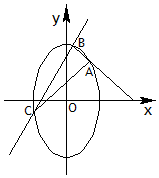 如图,点$A(1,\sqrt{3})$为椭圆$\frac{x^2}{2}+\frac{y^2}{n}=1$上一定点,过点A引两直线与椭圆分别交于B,C两点.
如图,点$A(1,\sqrt{3})$为椭圆$\frac{x^2}{2}+\frac{y^2}{n}=1$上一定点,过点A引两直线与椭圆分别交于B,C两点.