题目内容
1.已知函数f(x)=$\frac{3}{1+|x|}$+$\frac{3}{1+|x-2|}$,则方程f[f(x)]=$\frac{10}{3}$的实数解的个数是( )| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
分析 利用换元法,将方程进行转化,作出函数的图象,利用数形结合进行求解即可.
解答 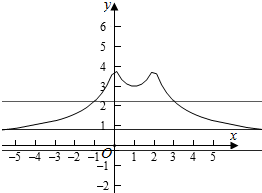 解:①当x≥2时,f(x)=$\frac{3}{1+x}$+$\frac{3}{1+x-2}$=$\frac{3}{1+x}$+$\frac{3}{x-1}$=$\frac{6x}{{x}^{2}-1}$,
解:①当x≥2时,f(x)=$\frac{3}{1+x}$+$\frac{3}{1+x-2}$=$\frac{3}{1+x}$+$\frac{3}{x-1}$=$\frac{6x}{{x}^{2}-1}$,
设t=f(x),则由f[f(x)]=$\frac{10}{3}$得f(t)=$\frac{10}{3}$,t≥2,
即$\frac{6t}{{t}^{2}-1}$=$\frac{10}{3}$,
即5t2-9t-5=0,得t=$\frac{9±\sqrt{181}}{10}$,此时t=$\frac{9+\sqrt{181}}{10}$.
②当0<x<2时,f(x)=$\frac{3}{1+x}$+$\frac{3}{1-x+2}$=$\frac{3}{1+x}$+$\frac{3}{3-x}$=-$\frac{12}{{x}^{2}-2x-3}$,
由f(t)=$\frac{10}{3}$,0<t<2,
得$-\frac{12}{{t}^{2}-2t-3}$=$\frac{10}{3}$,即5t2-10t+3=0,(0<t<2)
得t=$\frac{10+\sqrt{100-4×5×3}}{10}$=$\frac{10+\sqrt{40}}{10}=\frac{10+2\sqrt{10}}{10}$=$\frac{5+\sqrt{10}}{10}$或t=$\frac{5-\sqrt{10}}{10}$(舍).
③当x≤0时,f(x)=$\frac{3}{1-x}$+$\frac{3}{1-x+2}$=$\frac{3}{1-x}$+$\frac{3}{3-x}$=-$\frac{6(x-2)}{{x}^{2}-4x+3}$,
由f(t)=$\frac{10}{3}$,t≤0,
得$-\frac{6(t-2)}{{t}^{2}-4t+3}$=$\frac{10}{3}$,
即5t2-11t-3=0
得t=$\frac{11+\sqrt{181}}{10}$(舍)或t=$\frac{11-\sqrt{181}}{10}$.
作出f(x)的图象如图:
分别作出y=$\frac{9+\sqrt{181}}{10}$和y=$\frac{5+\sqrt{10}}{10}$和y=$\frac{11-\sqrt{181}}{10}$的图象,
由图象知,共有4个交点,即方程f[f(x)]=$\frac{10}{3}$的实数解的个数有4个,
故选:C.
点评 本题主要考查函数与方程的应用,利用换元法结合数形结合是解决本题的关键.综合性较强,难度较大.

| A. | 1 | B. | 3 | C. | 11 | D. | 13 |
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
| A. | y=cosx | B. | y=sinx | C. | y=lnx | D. | y=$\frac{1}{x}$ |