题目内容
已知二次函数f(x)=ax2+bx,且f(x+1)为偶函数,定义:满足f(x)=x的实数x称为函数f(x)不动点,若函数f(x)有且仅有一个不动点
(1)求f(x)的解析式;
(2)若函数g(x)=f(x)+
+
x2在(0,
]上是单调减函数,求实数k的取值范围;
(3)在(2)的条件下,讨论并求h(x)=x+
+1的零点.
(1)求f(x)的解析式;
(2)若函数g(x)=f(x)+
| k |
| x |
| 1 |
| 2 |
| ||
| 3 |
(3)在(2)的条件下,讨论并求h(x)=x+
| k |
| 4x |
考点:二次函数的性质,利用导数研究函数的单调性
专题:函数的性质及应用
分析:(1)由题意可得,二次函数f(x)=ax2+bx(a≠0)的对称轴为x=-
=1,故有b=-2a,再根据函数
f(x)有且仅有一个不动点,可得ax2 -2ax=x 只有一个解,由判别式等于零求得a、b的值,可得函数的解析式.
(2)g(x)=x+
,在(0,
]上是单调减函数,
得出答案.
(3)分类讨论得出当x>0时,h(x)>0恒成立,此时无零点,
根据对钩函数的性质得出:
当x<0时,f(x)max=1-
,
①当1-
=0时,即k=1时,h(x)有1个负零点,
②当k>1时,1-
<0,h(x)无零点,
③当
≤k<1时,1-
>0,h(x)有2个负零点,
| b |
| 2a |
f(x)有且仅有一个不动点,可得ax2 -2ax=x 只有一个解,由判别式等于零求得a、b的值,可得函数的解析式.
(2)g(x)=x+
| k |
| x |
| ||
| 3 |
|
(3)分类讨论得出当x>0时,h(x)>0恒成立,此时无零点,
根据对钩函数的性质得出:
当x<0时,f(x)max=1-
| k |
①当1-
| k |
②当k>1时,1-
| k |
③当
| 2 |
| 3 |
| k |
解答:
解:(1)由题意可得,二次函数f(x)=ax2+bx(a≠0)的对称轴为x=-
=1,∴b=-2a,
f(x)=ax2 -2ax.
再根据函数f(x)有且仅有一个不动点,可得ax2 -2ax=x 只有一个解,
故△=(2a+1)2-0=0,∴a=-
.
(2)f(x)=-
x2+x,
g(x)=f(x)+
+
x2,
∵即k≥
,
故实数k的取值范围:k≥
,
(3)h(x)=x+
+1,k≥
,
∵当x>0时,h(x)>0恒成立,
∴此时无零点,
∵当x<0时,-x-
≥2
=
,
∴x+
≤-
,
∴当x<0时,f(x)max=1-
,
∵k≥
①当1-
=0时,即k=1时,h(x)有1个负零点,
②当k>1时,1-
<0,h(x)无零点,
③当
≤k<1时,1-
>0,h(x)有2个负零点,
| b |
| 2a |
f(x)=ax2 -2ax.
再根据函数f(x)有且仅有一个不动点,可得ax2 -2ax=x 只有一个解,
故△=(2a+1)2-0=0,∴a=-
| 1 |
| 2 |
(2)f(x)=-
| 1 |
| 2 |
g(x)=f(x)+
| k |
| x |
| 1 |
| 2 |
∵即k≥
| 2 |
| 3 |
故实数k的取值范围:k≥
| 2 |
| 3 |
(3)h(x)=x+
| k |
| 4x |
| 2 |
| 3 |
∵当x>0时,h(x)>0恒成立,
∴此时无零点,
∵当x<0时,-x-
| k |
| 4x |
|
| k |
∴x+
| k |
| 4x |
| k |
∴当x<0时,f(x)max=1-
| k |
∵k≥
| 2 |
| 3 |
①当1-
| k |
②当k>1时,1-
| k |
③当
| 2 |
| 3 |
| k |
点评:本题考查了函数的性质,解析式的求解,函数的零点,分类讨论的思想,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,则满足f(a)≥2的实数a的取值范围是( )
|
| A、(-∞,-2)∪(0,+∞) |
| B、(-1,0) |
| C、(-2,0) |
| D、(-∞,-1]∪[0,+∞) |
运行如如图所示的程序框图,则输出的结果S为( )


| A、1008 | B、2015 |
| C、1007 | D、-1007 |
从半径为r的圆内接正方形的4个顶点及圆心5个点中任取2个点,则这个点间的距离小于或等于半径的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
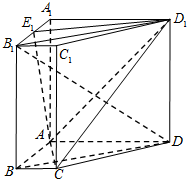 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=