题目内容
下列函数中,既是偶函数又在区间(-∞,0)上单调递增的是( )
A、f(x)=
| ||
| B、f(x)=x2+1 | ||
| C、f(x)=x3 | ||
| D、f(x)=2-x |
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:利用函数函数的奇偶性和单调性即可判断出.
解答:
解:只有函数f(x)=
,f(x)=x2+1是偶函数,而函数f(x)=x3是奇函数,f(x)=2-x不具有奇偶性.
而函数f(x)=
,f(x)=x2+1中,只有函数f(x)=
在区间(-∞,0)上单调递增的.
综上可知:只有A正确.
故选:A.
| 1 |
| x2 |
而函数f(x)=
| 1 |
| x2 |
| 1 |
| x2 |
综上可知:只有A正确.
故选:A.
点评:本题考查了函数函数的奇偶性和单调性,属于基础题.

练习册系列答案
相关题目
设样本数据x1,x2,…,x10的均值和方差分别为1和4,若yi=xi+a(a为非零常数,i=1,2,…,10),则y1,y2,…,y10的均值和方差分别为( )
| A、1+a,4 |
| B、1+a,4+a |
| C、1,4 |
| D、1,4+a |
执行如图所示的程序框图,输出的S值为( )


| A、1 | B、3 | C、7 | D、15 |
阅读如图所示的程序框图,运行相应的程序,输出的n的值为( )
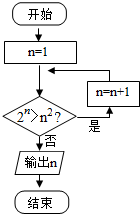

| A、1 | B、2 | C、3 | D、4 |
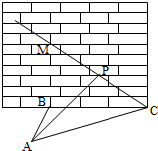 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练.已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是