题目内容
(x-1)10的展开式的第3项的系数是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:二项式定理的应用
专题:二项式定理
分析:利用二项式展开式的通项公式,求得展开式的第3项,可得展开式的第3项的系数.
解答:
解:(x-1)10的展开式的第3项为 T3=
•x8,
故第3项的系数是
,
故选:A.
| C | 2 10 |
故第3项的系数是
| C | 2 10 |
故选:A.
点评:本题主要考查二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
为了得到函数y=cos(x+
)的图象,只需要把函数y=cos(x-
)的图象上的所有点( )
| π |
| 4 |
| π |
| 4 |
A、向右平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向左平行移动
|
若
(3x2+kx)dx=3,则k=( )
| ∫ | 1 0 |
| A、1 | B、2 | C、3 | D、4 |
一个三角形的三边长依次是4、6、2
,这个三角形的面积等于( )
| 7 |
A、3
| ||
B、6
| ||
C、3
| ||
D、6
|
框图所示给出的程序,则程序结束时输出结果S为( )


| A、12 | B、10 | C、8 | D、6 |
如图,已知△ABC中,D为BC边上的中点,则下列等式中正确的是( )
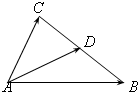

A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
△ABC中,a,b,c分别是角A,B,C所对的边,若A=75°,B=45°,c=2
,则b等于( )
| 3 |
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |