题目内容

在△ABC中，已知AC=
1
2
AB，CM是∠ACB的平分线，△AMC的外接圆交BC边于点N，求证：BN=2AM．
考点：与圆有关的比例线段
专题：证明题,立体几何
分析：因为CM是∠ACB的平分线，由内角平分线定理，可得
AC
BC
=
AM
BM
，再由圆的切割线定理，可得BM•BA=BN•BC，整理，即可得证．
解答： 证明：如图，在△ABC中，因为CM是∠ACB的平分线，
所以
AC
BC
=
AM
BM
．
又AC=
1
2
AB，所以
AB
AC
=
2AM
BM
 ①
因为BA与BC是圆O过同一点B的弦，
所以，BM•BA=BN•BC，即
AB
BC
=
NB
BM
②
由①、②可知 
2AM
BM
=
BN
BM
，
所以BN=2AM．
点评：本题考查内角平分线定理和圆的切割线定理及运用，考查推理能力，属于中档题．
练习册系列答案
相关题目
下列说法不正确的是（　　）
A、命题“对?x∈R，都有x2≥0”的否定为“?x0∈R，使得x02＜0”
B、“a＞b”是“ac2＞bc2”的必要不充分条件
C、“若tanα≠
3
，则α≠
π
3
”是真命题
D、甲、乙两位学生参与数学模拟考试，设命题p是“甲考试及格”，q是“乙考试及格”，则命题“至少有一位学生不及格”可表示为（￢p）∧（￢q）
已知幂函数f（x）=xα的图象过点(2，
2
2
)，则f（16）=
 
．
某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图如图所示．（每个分组包括左端点，不包括右端点，如第一组表示[1000，1500））

（Ⅰ）求居民收入在[1500，2500）的频率；
（Ⅱ）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析，则月收入在[2500，3000）的这段应抽取多少人？
已知圆C1：（x-2cosθ）2+（y-2sinθ）2=1与圆C2：x2+y2=1，在下列说法中：
①对于任意的θ，圆C1与圆C2始终相切；
②对于任意的θ，圆C1与圆C2始终有四条公切线；
③直线l：2（m+3）x+3（m+2）y-（2m+5）=0（m∈R）与圆C2一定相交于两个不同的点；
④P，Q分别为圆C1与圆C2上的动点，则|PQ|的最大值为4．
其中正确命题的序号为
 
．
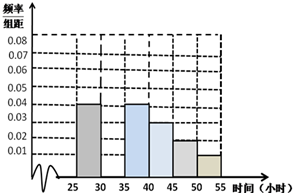教育部，体育总局和共青团中央号召全国各级各类学校要广泛，深入地开展全国亿万大，中学生阳光体育运动，为此，某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计，随机抽取了100名学生作为样本，得到这100名学生在该月参加体育运动总时间的小时数，根据此数据作出了如下的频数和频率的统计表和 频率分布直方图：
（I）求a，p的值，并补全频率分布直方图；
（Ⅱ）根据上述数据和直方图，试估计运动时间在[25，55]小时的学生体育运动的平均时间；
分组运动时间
（小时）		频数频率
1[25，30）200.2
2[30，35） ap
3[35，40）200.2
4[40，45）150.15
5[45，50）100.10
6[50，55]50.05
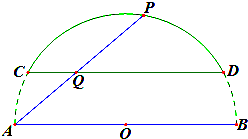某房地产开发商在其开发的一个小区前面建了一个弓形景观湖，如图，该弓形所在的圆是以AB为直径的圆，已知AB=300m，CD与AB平行且它们之间的距离为50
2
m，开发商计划从A点出发建一座景观桥（假定建成的景观桥与地面和湖面均平行），为了使小区居民可以充分的欣赏湖景，所以要将湖面上的景观桥PQ的长度设计到最长．
（1）记∠AOP=2θ，试用θ表示线段PQ；
（2）求PQ的最大值．
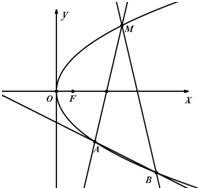已知点F为抛物线C：y2=2px（p＞0）的焦点，M（4，t）（t＞0）为抛物线C上的点，且|MF|=5．
（Ⅰ）求抛物线C的方程和点M的坐标；
（Ⅱ）过点M引出斜率分别为k1，k2的两直线l1，l2，l1与抛物线C的另一交点为A，l2与抛物线C的另一交点为B，记直线AB的斜率为k3．
（ⅰ）若k1+k2=0，试求k3的值；
（ⅱ）证明：
1
k1
+
1
k2
-
1
k3
为定值．
执行如图所示的程序框图，输出s的值等于（　　）
A、98B、100
C、2450D、2550

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网