题目内容
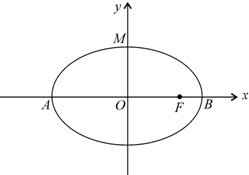 如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且
如图,椭圆长轴端点为A,B,O为椭圆中心,F为椭圆的右焦点,且| AF |
| FB |
| OF |
(1)求椭圆的标准方程;
(2)记椭圆的上顶点为M,直线l交椭圆于P,Q两点,问:是否存在直线l,使点F恰为△PQM的垂心?若存在,求出直线l的方程;若不存在,请说明理由.
分析:(1)设出椭圆的方程,根据题意可知c,进而根据
•
=1求得a,进而利用a和c求得b,则椭圆的方程可得.
(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,设出P,Q的坐标,利用点M,F的坐标求得直线PQ的斜率,设出直线l的方程,与椭圆方程联立,由韦达定理表示出x1+x2和x1x2,进而利用
•
=0求得m.
| AF |
| FB |
(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,设出P,Q的坐标,利用点M,F的坐标求得直线PQ的斜率,设出直线l的方程,与椭圆方程联立,由韦达定理表示出x1+x2和x1x2,进而利用
| MP |
| FQ |
解答:解.(1)如图建系,设椭圆方程为
+
=1(a>b>0),则c=1
 又∵
又∵
•
=1即(a+c)•(a-c)=1=a2-c2,∴a2=2
故椭圆方程为
+y2=1
(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,则
设P(x1,y1),Q(x2,y2),∵M(0,1),F(1,0),故kPQ=1,
于是设直线l为y=x+m,由
得3x2+4mx+2m2-2=0,
又F为△PQM的垂心,则MP⊥FQ,
故
•
=x1(x2-1)+y2(y1-1)=0又yi=xi+m(i=1,2)
得x1(x2-1)+(x2+m)(x1+m-1)=0即2x1x2+(x1+x2)(m-1)+m2-m=0由韦达定理得2•
-
(m-1)+m2-m=0
解得m=-
或m=1(舍)经检验m=-
符合条件,
此时直线l的方程为y=x-
.
| x2 |
| a2 |
| y2 |
| b2 |
 又∵
又∵| AF |
| FB |
故椭圆方程为
| x2 |
| 2 |
(2)假设存在直线l交椭圆于P,Q两点,且F恰为△PQM的垂心,则
设P(x1,y1),Q(x2,y2),∵M(0,1),F(1,0),故kPQ=1,
于是设直线l为y=x+m,由
|
又F为△PQM的垂心,则MP⊥FQ,
故
| MP |
| FQ |
得x1(x2-1)+(x2+m)(x1+m-1)=0即2x1x2+(x1+x2)(m-1)+m2-m=0由韦达定理得2•
| 2m2-2 |
| 3 |
| 4m |
| 3 |
解得m=-
| 4 |
| 3 |
| 4 |
| 3 |
此时直线l的方程为y=x-
| 4 |
| 3 |
点评:本题主要考查了直线与圆锥曲线的关系.考查了学生综合运用基础知识解决问题的能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 且
且 (本小题满分12分)如图,椭圆长轴端点为
(本小题满分12分)如图,椭圆长轴端点为 ,
, 为椭圆中心,
为椭圆中心,
 为椭圆的右焦点,
为椭圆的右焦点, ,
, .
.
 ,直线
,直线 交椭圆于
交椭圆于 两点,问:是否存在直线
两点,问:是否存在直线 的垂心?若存在,求出直线
的垂心?若存在,求出直线 ,
, 为椭圆中心,
为椭圆中心, 为椭圆的右焦点,且
为椭圆的右焦点,且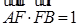 ,
,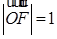 ;
; ,直线
,直线 交椭圆于
交椭圆于 两点,问:是否存在直线
两点,问:是否存在直线 的垂心?若存在,求出直线
的垂心?若存在,求出直线