题目内容
如图，椭圆长轴端点为
,
为椭圆中心，
为椭圆的右焦点,
且
，
.
(Ⅰ)求椭圆的标准方程；
(Ⅱ)记椭圆的上顶点为
，直线
交椭圆于
两点，问：是否存在直线，使点恰为
的垂心？若存在，求出直线的方程;若不存在，请说明理由
(Ⅰ) 
(Ⅱ) 
解析:
（1）设椭圆方程为
由题意
又∵即 
∴
故椭圆方程为
…………4分
（2）假设存在直线交椭圆于两点，且恰为的垂心，则
设
，∵
，故 
……………6分
于是设直线为 
，由
得
…………8分
∵
又
得
即
由韦达定理得
解得
或
（舍） 经检验符合条件
则直线的方程为:
………13分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
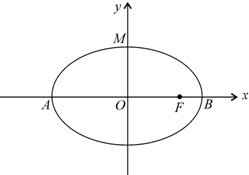如图，椭圆长轴端点为A，B，O为椭圆中心，F为椭圆的右焦点，且
（本小题满分12分）如图，椭圆长轴端点为
,
为椭圆中心，
为椭圆的右焦点,且
，
.(1)求椭圆的标准方程；(2)记椭圆的上顶点为
，直线
交椭圆于
两点，问：是否存在直线
的垂心？
，
为椭圆中心，
为椭圆的右焦点，
,
.
，直线
交椭圆于
两点，问：是否存在直线
的垂心？若存在，求出直线
，
为椭圆中心，
为椭圆的右焦点,且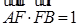
，
；
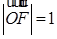，直线
交椭圆于
两点，问：是否存在直线
的垂心？若存在，求出直线