题目内容
（本题满分15分）
如图，椭圆长轴端点为
，
为椭圆中心，
为椭圆的右焦点,且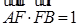
，
；
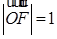（1）求椭圆的标准方程；
（2）记椭圆的上顶点为
，直线
交椭圆于
两点，问：是否存在直线，使点恰为
的垂心？若存在，求出直线的方程;若不存在，请说明理由.
【答案】
（1）
（2）
【解析】解：（1）如图建系，设椭圆方程为
,则
又∵
即 
∴
故椭圆方程为 …………6分
（2）假设存在直线
交椭圆于
两点，且
恰为
的垂心，则设
，∵
，故
， ……8分
于是设直线为 
，由
得
…………………………………10分
∵
又
得
即
由韦达定理得
解得或
（舍） 经检验符合条件………15分
练习册系列答案
相关题目
．
在
上单调递增，在
上单调递减，求实数
的最大值；
对任意的
，
都成立，求实数
的取值范围．
为自然对数的底数．
与曲线
相切
在
上恰有两个不等的实数根
，求
的大小
：
（
），焦点为
，直线
交抛物线
、
两点，
是线段
的中点，
轴的垂线交抛物线
，
到焦点
，求此时
的值；
是以
的单调区间；
，若
在
上不单调且仅在
处取得最大值，求
的取值范围．