题目内容
20.盒子中装有编号为1,2,3,4,5的5个球,从中有放回的取两次球,每次取一个,则这两次取出球的编号之积为偶数的概率为$\frac{16}{25}$.分析 取出的两个球的编号之积为偶数的情况有两种:取出一奇一偶两个数和取出两个偶数.由此能求出结果.
解答 解:从中有放回的取两次球,共有15种结果,满足条件的由有(1,2),(1,4),(2,1),(2,2),(2,3),(2,4),(2,5),(3,2),(3,4),(4,1),(4,2),(4,3),(4,4),(4,5),(5,2),(5,4),共16种.
故这两次取出球的编号之积为偶数的概率为$\frac{16}{25}$
故答案为:$\frac{16}{25}$
点评 本题考查概率的求法,解题时要认真审题,是基础题.

练习册系列答案
相关题目
15.若0<x1<x2,0<y1<y2,且x1+x2=y1+y2=1,则下列代数式中值最大的是( )
| A. | x1y1+x2y2 | B. | x1x2+y1y2 | C. | x1y2+x2y1 | D. | $\frac{1}{2}$ |
10.已知全集U=R,集合A={x|2<x≤3},集合B={x|2≤x≤4},则(∁UA)∩B等于( )
| A. | {x|3≤x≤4} | B. | {x|3<x≤4} | C. | {x|x=2或3<x≤4} | D. | {x|3<x<4} |
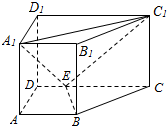 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD=$\sqrt{2}$,AA1=3,E为CD上一点,DE=1,EC=3.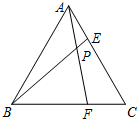 等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.
等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连结AF,BE相交于点P.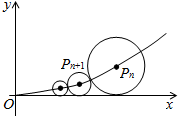 在xOy平面上有一系列点P1(x1,y1),P2(x2,y2),…Pn(xn,yn)对每个正整数n,点Pn位于函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与H轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xn(n∈N+).
在xOy平面上有一系列点P1(x1,y1),P2(x2,y2),…Pn(xn,yn)对每个正整数n,点Pn位于函数y=x2(x≥0)的图象上,以点Pn为圆心的圆Pn与H轴都相切,且圆Pn与圆Pn+1又彼此外切.若x1=1,且xn+1<xn(n∈N+).