题目内容
5.已知函数f(x)=x2-cosx,$x∈[-\frac{π}{2},\;\frac{π}{2}]$,则满足$f({x_0})<f(\frac{π}{3})$的x0的取值范围是(-$\frac{π}{3}$,$\frac{π}{3}$).分析 由条件利用函数的图象特征,余弦函数的奇偶性和单调性,数形结合求得结论.
解答  解:函数f(x)=x2-cosx,$x∈[-\frac{π}{2},\;\frac{π}{2}]$为偶函数,
解:函数f(x)=x2-cosx,$x∈[-\frac{π}{2},\;\frac{π}{2}]$为偶函数,
则且函数在[0,$\frac{π}{2}$]上单调递增,
如图所示:
结合图象可得满足$f({x_0})<f(\frac{π}{3})$的x0的取值范围是
$(-\frac{π}{3},\frac{π}{3})$,
故答案为:(-$\frac{π}{3}$,$\frac{π}{3}$).
点评 本题主要考查函数的图象特征,余弦函数的奇偶性和单调性,属于中档题.

练习册系列答案
相关题目
17.已知b是实数,若$\frac{1+bi}{2-i}$是纯虚数,则b=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
15.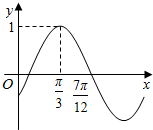 已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cosωx的图象( )
已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cosωx的图象( )
 已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cosωx的图象( )
已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cosωx的图象( )| A. | 向右平移$\frac{π}{3}$个长度单位 | B. | 向左平移$\frac{π}{3}$个长度单位 | ||
| C. | 向右平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{6}$个长度单位 |
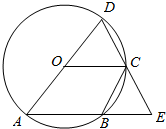 如图,AD是⊙O的直径,B为⊙O上的一点,连接AB并延长至点E,使得AE=AD,连接DE,交⊙O于点C,连接OC.
如图,AD是⊙O的直径,B为⊙O上的一点,连接AB并延长至点E,使得AE=AD,连接DE,交⊙O于点C,连接OC.