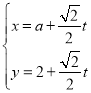题目内容
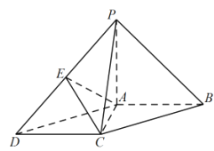
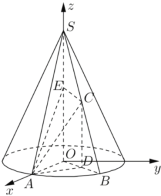
【题目】如图所示,圆锥的底面![]() 半径为2,
半径为2,![]() 是圆周上的定点,动点
是圆周上的定点,动点![]() 在圆周上逆时针旋转,设
在圆周上逆时针旋转,设![]() (
(![]() ),
),![]() 是母线
是母线![]() 的中点,已知当
的中点,已知当![]() 时,
时,![]() 与底面所成角为
与底面所成角为![]() .
.
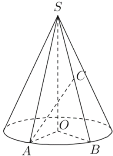
(1)求该圆锥的侧面积;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() .(2)
.(2)![]() 或
或![]() .
.
【解析】
(1)作出![]() 与底面所成角
与底面所成角![]() ,利用
,利用![]() ,由此求得
,由此求得![]() ,进而求得圆锥的侧面积.
,进而求得圆锥的侧面积.
(2)解法一:建立空间直角坐标系,利用![]() 求得
求得![]() 的值,进而求得
的值,进而求得![]() 的值.
的值.
解法二:判断出三角形![]() 是等边三角形,由此求得
是等边三角形,由此求得![]() 的值.
的值.
解法三:通过构造直角三角形的方法,求得![]() 的值,进而求得
的值,进而求得![]() 的值.
的值.
(1)![]() ,
,![]() ,
,
设![]() 为
为![]() 中点,连接
中点,连接![]() ,则
,则![]() ∥
∥![]() ,
,
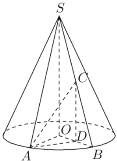
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]()
在Rt△![]() 中,
中,![]() ,
,![]() ,得:
,得:![]() ,
,
得:![]() ,
,![]() ,
,
∴![]() ,
,
![]() .
.
(2)解法一:如图建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
由题意,![]() ,
,
∵![]() ,∴
,∴![]() 或
或![]() .
.
解法二:设![]() 为
为![]() 中点,连接
中点,连接![]() ,则
,则![]() ∥
∥![]() , ∴
, ∴![]() ,
,
又∵![]() ,可得:
,可得:![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴△![]() 是等边三角形,
是等边三角形,
∴![]() 或
或![]() .
.
解法三:设![]() 为
为![]() 中点,连接
中点,连接![]()
![]() ,∴
,∴![]()
设![]() 为
为![]() 中点,连接
中点,连接![]()
![]() ,∴
,∴![]() ,
,
在△![]() 中,由余弦定理有:
中,由余弦定理有:![]() ,
,
∴在Rt△![]() 中,
中,![]() ,在△
,在△![]() 中,
中,![]() ,
,
∴在Rt△![]() 中,
中,![]() ,即得
,即得![]() ,
,
∵![]() ,∴
,∴![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】为助力湖北新冠疫情后的经济复苏,某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根据以上数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该产品成本是4元/件,假设该产品全部卖出,预测把单价定为多少时,工厂获得最大利润?
(参考公式:回归方程![]() ,其中
,其中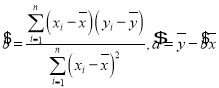 )
)