题目内容
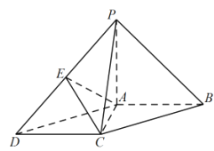
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为平行四边形,
为平行四边形,![]() ,且
,且![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)在线段![]() 上(不含端点)是否存在一点
上(不含端点)是否存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,确定
?若存在,确定![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)证明见解析.(2)![]() .(3)存在,
.(3)存在,![]()
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,可证
,可证![]() ,从而得线面平行;
,从而得线面平行;
(2)由题意以![]() 为坐标原点,分别以
为坐标原点,分别以![]()
![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,可用向量法求出线面角;
轴建立空间直角坐标系,可用向量法求出线面角;
(3)在(2)基础上,设![]() ,求出平面
,求出平面![]() 和平面
和平面![]() ((2)中已有)法向量,由法向量夹角与二面角的关系可求得
((2)中已有)法向量,由法向量夹角与二面角的关系可求得![]() .
.
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
∵![]() 是平行四边形,∴
是平行四边形,∴![]() 是
是![]() 的中点.又
的中点.又![]() 是
是![]() 的中点,∴
的中点,∴![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;
;
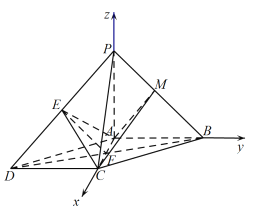
(2)以![]() 为坐标原点,分别以
为坐标原点,分别以![]()
![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() .
.
∵![]() ,
,
∴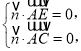 即
即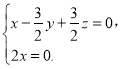
不妨取![]() ,得
,得![]()
又![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则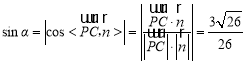 ,
,
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)假设在线段![]() 上(不含端点)存在一点
上(不含端点)存在一点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() .连接
.连接![]() .设
.设![]() , 得
, 得![]() .
.
设平面![]() 的法向量为
的法向量为![]() .
.
∵![]() ,
,
∴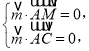 即
即![]()
不妨取![]() ,得
,得![]()
设二面角![]() 的平面角为
的平面角为![]() ,
,
则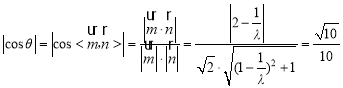 .
.
化简得![]() ,
,
解得![]() ,或
,或![]() .
.
∵二面角![]() 的余弦值为
的余弦值为![]() ,
,
∴![]() .
.
∴在线段![]() 上存在一点
上存在一点![]() ,且
,且![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】近年来,随着全球石油资源紧张、大气污染日益严重和电池技术的提高,电动汽车已被世界公认为21世纪汽车工业改造和发展的主要方向.为了降低对大气的污染和能源的消耗,某品牌汽车制造商研发了两款电动汽车车型![]() 和车型
和车型![]() ,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情况,制造商随机调查了5家汽车
,并在黄金周期间同时投放市场.为了了解这两款车型在黄金周的销售情况,制造商随机调查了5家汽车![]() 店的销量(单位:台),得到下表:
店的销量(单位:台),得到下表:
| 甲 | 乙 | 丙 | 丁 | 戊 |
车型 | 6 | 6 | 13 | 8 | 11 |
车型 | 12 | 9 | 13 | 6 | 4 |
(1)若从甲、乙两家![]() 店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的2台电动汽车中至少有1台是车型
店销售出的电动汽车中分别各自随机抽取1台电动汽车作满意度调查,求抽取的2台电动汽车中至少有1台是车型![]() 的概率;
的概率;
(2)现从这5家汽车![]() 店中任选3家举行促销活动,用
店中任选3家举行促销活动,用![]() 表示其中车型
表示其中车型![]() 销量超过车型
销量超过车型![]() 销量的
销量的![]() 店的个数,求随机变量
店的个数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2018年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示
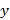
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2019年3月份的利润;
的线性回归方程,并预测该公司2019年3月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有![]() ,
,![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用
两种型号的新型材料可供选择,按规定每种新型材料最多可使用![]() 个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对
个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对![]() ,
,![]() 两种型号的新型材料对应的产品各
两种型号的新型材料对应的产品各![]() 件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
使用寿命 材料类型 |
|
|
|
| 总计 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的负责人,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .参考公式:回归直线方程为
.参考公式:回归直线方程为![]() ,其中
,其中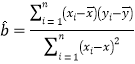
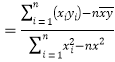 .
.