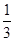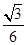题目内容
(本题满分14分)设 为非负实数,函数
为非负实数,函数 .
.
(Ⅰ)当 时,求函数的单调区间;
时,求函数的单调区间;
(Ⅱ)讨论函数 的零点个数.
的零点个数.
 为非负实数,函数
为非负实数,函数 .
.(Ⅰ)当
 时,求函数的单调区间;
时,求函数的单调区间;(Ⅱ)讨论函数
 的零点个数.
的零点个数.(Ⅰ)  的单调递增区间是
的单调递增区间是 和
和 ,单调递减区间是
,单调递减区间是 .
.
(Ⅱ)当 时,函数有一个零点;
时,函数有一个零点;
当 时,函数有两个零点;
时,函数有两个零点;
当 时,函数有三个零点.
时,函数有三个零点.
 的单调递增区间是
的单调递增区间是 和
和 ,单调递减区间是
,单调递减区间是 .
. (Ⅱ)当
 时,函数有一个零点;
时,函数有一个零点;当
 时,函数有两个零点;
时,函数有两个零点;当
 时,函数有三个零点.
时,函数有三个零点. 试题分析:(Ⅰ)当
 时,
时, ,然后对于分段函数各段的情况分别说明单调性,整体来合并得到结论。
,然后对于分段函数各段的情况分别说明单调性,整体来合并得到结论。(2)当
 时,
时, ,
,故当
 时,
时, ,二次函数对称轴
,二次函数对称轴 ,那么结合二次函数的 性质可知顶点的函数值为正数,负数,还是零,来确定零点的问题。
,那么结合二次函数的 性质可知顶点的函数值为正数,负数,还是零,来确定零点的问题。解:(Ⅰ)当
 时,
时, ,
,① 当
 时,
时, ,∴
,∴ 在
在 上单调递增;
上单调递增;② 当
 时,
时, ,
,∴
 在
在 上单调递减,在
上单调递减,在 上单调递增;
上单调递增;综上所述,
 的单调递增区间是
的单调递增区间是 和
和 ,单调递减区间是
,单调递减区间是 .
. (Ⅱ)(1)当
 时,
时, ,函数
,函数 的零点为
的零点为 ;
; (2)当
 时,
时, ,
,故当
 时,
时, ,二次函数对称轴
,二次函数对称轴 ,
,∴
 在
在 上单调递增,又
上单调递增,又 ,f(x)与x轴在
,f(x)与x轴在 有唯一交点;
有唯一交点;当
 时,
时, ,二次函数对称轴
,二次函数对称轴 ,
,∴
 在
在 上单调递减,在
上单调递减,在 上单调递增;∴
上单调递增;∴ ,
,  当
当 ,即
,即 时,函数
时,函数 与
与 轴只有唯一交点,即唯一零点,
轴只有唯一交点,即唯一零点, 当
当 ,即
,即 时,函数
时,函数 与
与 轴有两个交点,即两个零点
轴有两个交点,即两个零点 当
当 ,即
,即 时,f(a)<0,函数
时,f(a)<0,函数 与
与 轴有三个交点,即有三个零点
轴有三个交点,即有三个零点综上可得,当
 时,函数有一个零点;
时,函数有一个零点;当
 时,函数有两个零点;
时,函数有两个零点;当
 时,函数有三个零点.
时,函数有三个零点. 点评:解决该试题的关键是对于参数的分类讨论是否能够很好的全面的表示出不同情况下的零点,也是该试题一个难点。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和
和 ,定义运算“﹡”:
,定义运算“﹡”: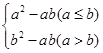 ,设
,设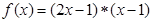 且关于
且关于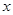 的方程
的方程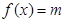 (
(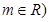 恰有三个互不相等的实根
恰有三个互不相等的实根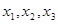 ,则
,则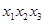 的取值范围是 。
的取值范围是 。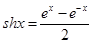 和双曲余弦函数
和双曲余弦函数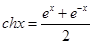 ,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 。
,双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有许多相类似的性质,请类比正、余弦函数的和角或差角公式,写出关于双曲正弦、双曲余弦函数的一个正确的类似公式 。
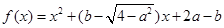 是偶函数,则函数图像与
是偶函数,则函数图像与 轴交点的纵坐标的最大值是( ).
轴交点的纵坐标的最大值是( ). },B={y|1
},B={y|1 },下列图形表示集合A到集合B的函数图形的是( )
},下列图形表示集合A到集合B的函数图形的是( )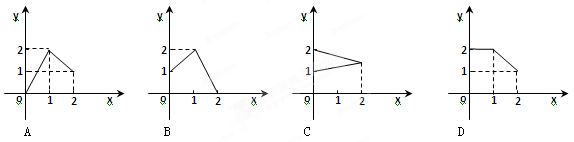
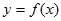 ,若同时满足下列条件:①
,若同时满足下列条件:①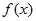 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[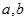 ]
]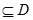 ,使
,使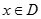 )叫闭函数.
)叫闭函数.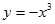 符合条件②的区间[
符合条件②的区间[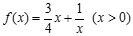 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;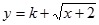 是闭函数,求实数
是闭函数,求实数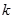 的取值范围.
的取值范围.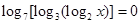 ,那么
,那么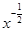 等于( )
等于( )