题目内容
(本小题满分12分)
对于定义域为D的函数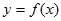 ,若同时满足下列条件:①
,若同时满足下列条件:①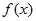 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[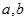 ]
]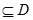 ,使
,使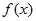 在[
在[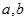 ]上的值域为[
]上的值域为[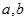 ];那么把
];那么把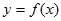 (
(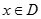 )叫闭函数.
)叫闭函数.
(1)求闭函数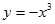 符合条件②的区间[
符合条件②的区间[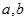 ];
];
(2)判断函数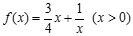 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若函数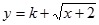 是闭函数,求实数
是闭函数,求实数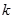 的取值范围.
的取值范围.
对于定义域为D的函数
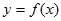 ,若同时满足下列条件:①
,若同时满足下列条件:①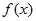 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[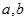 ]
]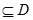 ,使
,使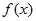 在[
在[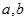 ]上的值域为[
]上的值域为[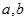 ];那么把
];那么把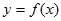 (
(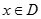 )叫闭函数.
)叫闭函数.(1)求闭函数
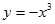 符合条件②的区间[
符合条件②的区间[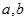 ];
];(2)判断函数
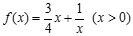 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;(3)若函数
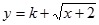 是闭函数,求实数
是闭函数,求实数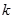 的取值范围.
的取值范围.(1)[-1,1]。(2)函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。(3)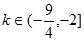 。
。
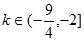 。
。试题分析:(1)根据y=-x3的单调性,假设区间为[a,b]满足,求a、b的值.
(2)取一特殊值x1=1,x2=10,代入验证不满足条件即可证明不是闭函数.
(3)根据闭函数的定义,得到a,b,k的关系式,然后转换为方程有两个不等的实数根来得到参数的范围。
解:
(1)由题意,
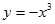 在[
在[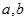 ]上递减,则
]上递减,则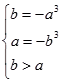 解得
解得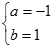
所以,所求的区间为[-1,1]..............................................2分
(2)
取
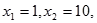 则
则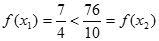 ,
,即
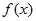 不是
不是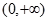 上的减函数。
上的减函数。取
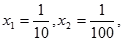
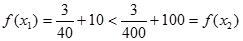 ,
,即
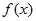 不是
不是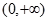 上的增函数,
上的增函数,所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。.............4分
(3)若
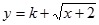 是闭函数,则存在区间[
是闭函数,则存在区间[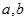 ],在区间[
],在区间[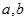 ]上,函数
]上,函数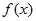 的值域为[
的值域为[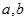 ],即
],即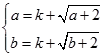 ,
, 为方程
为方程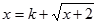 的两个实根,
的两个实根,即方程
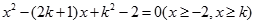 有两个不等的实根。
有两个不等的实根。当
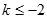 时,有
时,有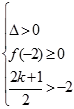 ,解得
,解得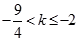 。...............................7分
。...............................7分当
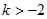 时,有
时,有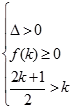 ,无解。........................................10分
,无解。........................................10分综上所述,
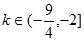 ....................................12分
....................................12分点评:解决该试题的关键是理解闭函数的概念,并能结合所学知识,转换为不等式以及对应的函数关系式。

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
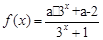 .
. 
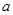 使函数f(x)为奇函数?证明你的结论;
使函数f(x)为奇函数?证明你的结论;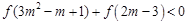 .
.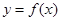 是定义在
是定义在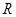 上的奇函数,当
上的奇函数,当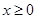 时,
时,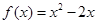 ,则在
,则在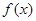 的表达式为
的表达式为 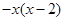
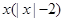
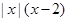
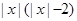
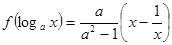
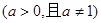
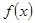 ;
;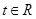 ,不等式
,不等式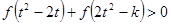 恒成立,求
恒成立,求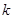 的取值范围。
的取值范围。 为非负实数,函数
为非负实数,函数 .
. 时,求函数的单调区间;
时,求函数的单调区间; 的零点个数.
的零点个数.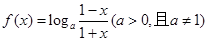
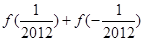 的值;
的值;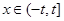 (其中
(其中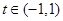 ,且
,且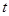 为常数)时,
为常数)时,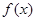 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如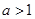 时,求满足不等式
时,求满足不等式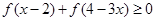 的
的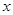 的范围.
的范围.  。
。 ,使不等式
,使不等式 能成立,求实数
能成立,求实数 的最小值;
的最小值; 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数 的取值范围。
的取值范围。
 恒成立,求m的取值范围
恒成立,求m的取值范围 图像的是( )
图像的是( )