题目内容
设实数x,y满足不等式组
,则z=
的取值范围是 .
|
| x+2y |
| 2x+y |
考点:简单线性规划
专题:不等式的解法及应用
分析:考查约束条件表示的可行域,求出四个交点的坐标,通过换元法化简目标函数,求出斜率的范围,然后求解目标函数的范围即可.
解答:
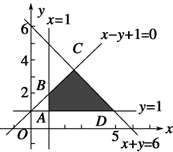 解:作出满足x≥1,y≥1,x+y≤6,x-y+1≥0的可行域如图中的阴影部分,四个顶点的坐标分别为A(1,1)、B(1,2)、C(
解:作出满足x≥1,y≥1,x+y≤6,x-y+1≥0的可行域如图中的阴影部分,四个顶点的坐标分别为A(1,1)、B(1,2)、C(
,
)、D(5,1),
将目标函数变形为z=
=
,令k=
,
则z=
,而k=
表示可行域中的点(x,y)与原点连线的斜率,数形结合易得可行域中的点D、B与原点连线的斜率分别取得最小值、最大值,故k=
∈[
,2],再由函数的性质易得z∈[
,
].
故答案为:[
,
].
 解:作出满足x≥1,y≥1,x+y≤6,x-y+1≥0的可行域如图中的阴影部分,四个顶点的坐标分别为A(1,1)、B(1,2)、C(
解:作出满足x≥1,y≥1,x+y≤6,x-y+1≥0的可行域如图中的阴影部分,四个顶点的坐标分别为A(1,1)、B(1,2)、C(| 5 |
| 2 |
| 7 |
| 2 |
将目标函数变形为z=
| x+2y |
| 2x+y |
1+
| ||
2+
|
| y |
| x |
则z=
| 1+2k |
| 2+k |
| y |
| x |
| y |
| x |
| 1 |
| 5 |
| 7 |
| 11 |
| 5 |
| 4 |
故答案为:[
| 7 |
| 11 |
| 5 |
| 4 |
点评:在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.注意转化思想的应用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
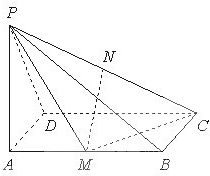 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°,AB=2,AD=1. 如图,已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,PA⊥平面ABCD,PA=2,∠ABC=60°,E、F分别为BC、PD的中点.
如图,已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,PA⊥平面ABCD,PA=2,∠ABC=60°,E、F分别为BC、PD的中点.