题目内容

5．由a1=1，d=3确定的等差数列{an}，当an=298，序号n等于（　　）
A．96B．98C．100D．101

分析 先求出等差数列的通项公式，由此能求出项数n．

解答 解：∵等差数列{an}中，a1=1，d=3
∴an=1+（n-1）×3=3n-2，
∵an=298，
∴an=3n-2=298，
解得n=100．
故选：C．

点评 本题考查等差数列的项数的求法，考查等差数列的通项公式等基础知识，考查运算求解能力，考查函数与方程思想，是基础题．

练习册系列答案
相关题目
19．若x，y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≤0}\\{x+2y-4≥0}\end{array}\right.$，则z=x+3y的最大值为10．．
20．在△ABC 中，a，b，c分别是内角A，B，C的对边，且acos2$\frac{C}{2}$+ccos2$\frac{A}{2}$=$\frac{3b}{2}$．
（Ⅰ）求证：a，b，c 成等差数列；
（Ⅱ）若B=$\frac{π}{3}$，b=4，求△ABC 的面积．
13．已知{an}为等比数列，a4+a7=2，a2a9=-8，则a1+a10=（　　）
A．7B．5C．-7D．-5
20．如图，在正方体ABCD-A1B1C1D1中，点P在正方体表面运动，如果${S_{△AB{D_1}}}={S_△}_{PB{D_1}}$，那么这样的点P共有（　　）
A．2个B．4个C．6个D．无数个
10．已知sin（30°+α）=$\frac{4}{5}$，60°＜α＜150°，则cosα=$\frac{4-3\sqrt{3}}{10}$．
17．已知m∈N*，则乘积m（m+1）（m+2）…（m+15）可表示为（　　）
A．A${\;}_{m}^{15}$B．A${\;}_{m}^{16}$C．A${\;}_{m+15}^{15}$D．A${\;}_{m+15}^{16}$
14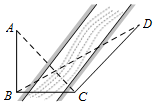．如图，某人为测量河对岸塔AB的高，先在塔底B的正东方向上的河岸上选一点C，在点C处测得点A的仰角为45°，并在点C北偏东15°方向的河岸上选定一点D，测得CD的距离为20米，∠BDC=30°，则塔AB的高是（　　）
A．10米B．$10\sqrt{2}$米C．$10\sqrt{3}$米D．$20\sqrt{3}$米
18．已知z=$\frac{3}{1+{i}^{2017}}$复数（i为虚数单位），则复数z的共轭复数在复平面内对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网