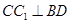题目内容
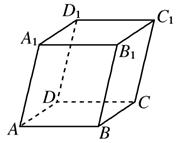
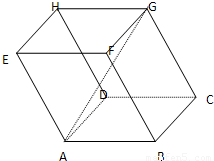
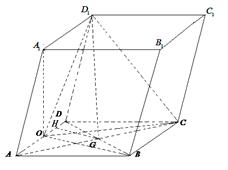
如图,平行六面体ABCD—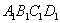 中,底面ABCD是边长为2的菱形,∠BAD=
中,底面ABCD是边长为2的菱形,∠BAD=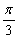 ,
,
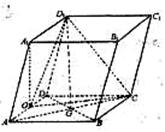 其中AC与BD交于点G,
其中AC与BD交于点G,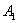 点在面ABCD上的射影0恰好为线段AD的中点。
点在面ABCD上的射影0恰好为线段AD的中点。
(I)求点G到平面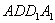 距离;
距离;
(Ⅱ)若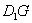 与平面
与平面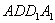 所成角的正弦值为
所成角的正弦值为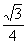 ,
,
求二面角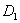 -OC-D的大小.
-OC-D的大小.
【答案】
解:(Ⅰ) 连结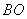 ,取
,取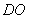 中点
中点 ,连结
,连结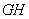 ,
,
 因为
因为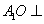 平面
平面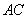 ,所以平面
,所以平面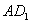
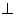 平面
平面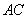 ,
,
又底面为菱形, 为
为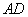 中点,
中点,
所以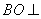 平面
平面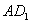 ,
,
因为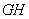 ∥
∥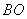 ,
,
所以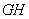
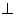 平面
平面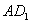 ,
,
又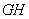 =
=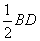 =
=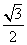 ,
,
所以点 到平面
到平面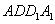 的距离为
的距离为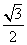 .
.
(Ⅱ)方法一:
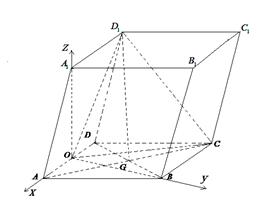 分别以
分别以 所在直线为
所在直线为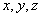 轴,建立如图所示的坐标系,
轴,建立如图所示的坐标系,
则 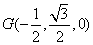 ,
,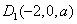 ,所以
,所以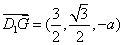 ,
,
面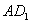 的一个法向量
的一个法向量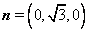 ,
,
所以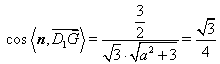 ,解得
,解得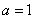 ,
,
因为面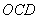 的一个法向量为
的一个法向量为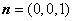 ,
,
设面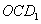 的一个法向量为
的一个法向量为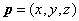 ,则
,则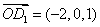 ,
,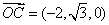 ,
,
则有 所以
所以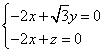 ,
,
取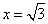 ,
,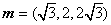 ,
,
 则
则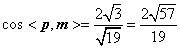 ,
,
所以二面角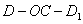 的大小为
的大小为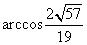 .
.
方法二:连结 ,由(1)可知
,由(1)可知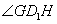 为直线
为直线
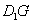 与平面
与平面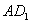 所成角.
所成角.
则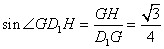 ,
,
所以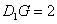
过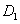 做
做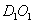 垂直
垂直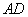 ,交其延长线于
,交其延长线于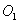 点,连结
点,连结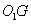 ,在
,在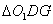 中,
中,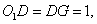
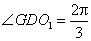 ,所以
,所以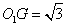 ,
,
那么在直角三角形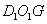 ,
,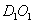 =1,
=1,
过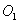 做
做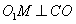 于点
于点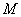 ,连结
,连结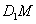 ,
,
则 为所求二面角的平面角,
为所求二面角的平面角,
连结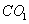 ,则
,则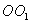
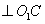 ,且
,且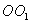 =2,
=2,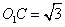 ,
,
则在△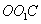 中,
中,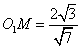 ,
,
所以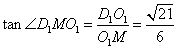 ,
,
所以所求二面角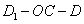 的大小为
的大小为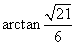 。
。

练习册系列答案
相关题目
 如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为
如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为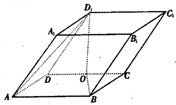 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.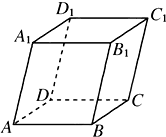 如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,