题目内容
在等差数列{an}中,a1=-8,它的前16项的平均值为7,若从中抽取一项,余下的15项的平均值是
,则抽取的是( )
| 36 |
| 5 |
| A、第7项 | B、第8项 |
| C、第15项 | D、第16项 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:易得抽取的项为4,由求和公式可得公差d=2,再由通项公式易得答案.
解答:
解:由题意可得抽取的项为16×7-15×
=4,
设等差数列{an}的公差为d,则数列的前16项和
S16=-8×16+
d=16×7,解得d=2,
设4为数列的第n项,则-8+2(n-1)=4,解得n=7
故选:A
| 36 |
| 5 |
设等差数列{an}的公差为d,则数列的前16项和
S16=-8×16+
| 16×15 |
| 2 |
设4为数列的第n项,则-8+2(n-1)=4,解得n=7
故选:A
点评:本题考查等差数列的通项公式和求和公式,属基础题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
已知椭圆的一个焦点为F(0,1),离心率e=
,则该椭圆的标准程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2+
|
设A、B为椭圆
+
=1上任意两点,O为坐标原点,则“OA⊥OB”是“O到直线AB的距离为
”的( )
| x2 |
| 16 |
| y2 |
| 9 |
| 12 |
| 5 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
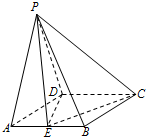 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PA=PD=3,PD⊥CD.E为AB中点.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PA=PD=3,PD⊥CD.E为AB中点.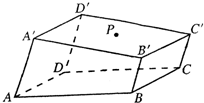 如图所示的一块木料中,棱BC平行于面A′C′.
如图所示的一块木料中,棱BC平行于面A′C′.