题目内容
已知tan(7π+α)=-2.
(1)求
的值;
(2)若α是第二象限角,求
的值.
(1)求
| cos2α-2sin2α |
| sin2α+3cos2α |
(2)若α是第二象限角,求
sin(π-α)cos(
| ||
sin(4π-α)sin(
|
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:计算题
分析:先化简tan(7π+α)=-2,求出tanα的值,再把(1)、(2)化简并弦化切,灵活利用同角的平方关系,即可计算出正确的答案.
解答:
解:∵tan(7π+α)=-2,
∴tanα=-2;
∴(1)
=
=
=
=-1;
(2)
=
=
=
=
=
=-3.
∴tanα=-2;
∴(1)
| cos2α-2sin2α |
| sin2α+3cos2α |
| 1-2tan2α |
| tan2α+3 |
=
| 1-2×(-2)2 |
| (-2)2+3 |
=
| 1-8 |
| 4+3 |
=-1;
(2)
sin(π-α)cos(
| ||
sin(4π-α)sin(
|
| sinα•(-sinα)-tanα |
| -sinα•(-cosα) |
=
| -sin2α-tanα |
| sinαcosα |
=
| ||
|
=
| ||
|
=
| ||
|
=-3.
点评:本题考查了同角的三角函数的基本关系的应用问题,解题时应灵活运用弦化切以及平方关系,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等差数列{an}中,a1=-8,它的前16项的平均值为7,若从中抽取一项,余下的15项的平均值是
,则抽取的是( )
| 36 |
| 5 |
| A、第7项 | B、第8项 |
| C、第15项 | D、第16项 |
双曲线的焦点在y轴上,且它的一个焦点在直线5x-2y+20=0上,两焦点关于原点对称.
=
,则此双曲线的方程是( )
| c |
| a |
| 5 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在直线y=2x+1上有一点P,过点P且垂直于直线4x+3y-3=0的直线与圆x2+y2-2x=0有公共点,则点P的横坐标的取值范围是( )
| A、(-∞,-1)∪(1,+∞) | ||||
| B、(-1,1) | ||||
C、[-
| ||||
D、(-
|
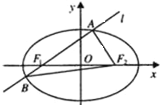 如图,椭圆
如图,椭圆