题目内容
7.已知:在四面体ABCD中,E、H,分别为棱AB、AD上靠近点A$\frac{1}{3}$的分点,F、G分别是BC、CD上的中点,判断四边形EFGH的形状并证明.分析 由已知得EH∥BD,且EH=$\frac{1}{3}BD$,GF∥BD,且GF=$\frac{1}{2}BD$,由此能证明四边形EFGH是梯形.
解答  解:四边形EFGH是梯形.
解:四边形EFGH是梯形.
证明如下:
∵在四面体ABCD中,E、H,分别为棱AB、AD上靠近点A$\frac{1}{3}$的分点,
∴EH∥BD,且EH=$\frac{1}{3}BD$,
∵F、G分别是BC、CD上的中点,
∴GF∥BD,且GF=$\frac{1}{2}BD$,
∴EH∥FG,且EH<FG,
∴四边形EFGH是梯形.
点评 本题考查四边形形状的判断,是基础题,解题时要认真审题,注意空间思维能力和平行公理的合理运用.

练习册系列答案
相关题目
2.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是( )
| A. | BC∥平面PDF | B. | DF⊥平面PAE | C. | 平面PDE⊥平面ABC | D. | 平面PDF⊥平面PAE |
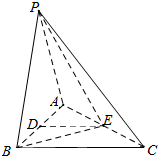 如图,在三棱锥P-ABC中,点D为AB上一点,点E为AC的中点,PA=PB=AB,BC=$\sqrt{2}$PE,∠PED=45°,DE∥平面PBC.
如图,在三棱锥P-ABC中,点D为AB上一点,点E为AC的中点,PA=PB=AB,BC=$\sqrt{2}$PE,∠PED=45°,DE∥平面PBC.



 如图所示.在120°的二面角α-AB-β中AC?α,BD?β,且AC⊥AB,BD⊥AB,垂足分别为A、B,已知AC=AB=BD=6,试求线段CD的长.
如图所示.在120°的二面角α-AB-β中AC?α,BD?β,且AC⊥AB,BD⊥AB,垂足分别为A、B,已知AC=AB=BD=6,试求线段CD的长.