题目内容
11.已知函数f(x)=$\frac{-3x-7}{x+2},g(x)={x^2}$-2x,若存在实数a∈(-∞,-2),使得f(a)+g(b)=0成立,则实数b的取值范围是(-1,3).分析 函数f(x)=-3-$\frac{1}{x+2}$,f(x)在x<-2上单调递减,求出f(x)的值域;存在实数a∈(-∞,-2),使得f(a)+g(b)=0成立即f(a)=-g(b)=2b-b2>-3.
解答 解:函数f(x)=$\frac{-3x-7}{x+2}$,x∈(-∞,-2)
函数f(x)=-3-$\frac{1}{x+2}$,f(x)在x<-2上单调递减;
所以f(x)∈(-3,+∞);
存在实数a∈(-∞,-2),使得f(a)+g(b)=0成立即f(a)=-g(b)=2b-b2>-3;
解得-1<b<3.
故答案为:(-1,3).
点评 本题主要考查了函数值域求法,以及恒成立问题与转化思想,属中等题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目
1.已知f(x)的定义域是(0,+∞),f'(x)为f(x)的导函数,且满足f(x)<f'(x),则不等式${e^{-x}}f({{x^2}+x})>{e^{{x^2}-2}}$f(2)的解集是( )
| A. | (-∞,2)∪(1,+∞) | B. | (-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (-1,2) |
2.已知函数$f(x)=\frac{2}{4^x}-x$,设a=0.2-2,b=log0.42,c=log43,则有( )
| A. | f(a)<f(c)<f(b) | B. | f(c)<f(b)<f(a) | C. | f(a)<f(b)<f(c) | D. | f(b)<f(c)<f(a) |
6.已知函数$f(x)=\left\{\begin{array}{l}{2^x}-2,x≥0\\{log_{\frac{1}{2}}}({-x}),x<0\end{array}\right.$,若f[f(m)]<0,则实数m的取值范围为( )
| A. | $({-3,-1}]∪({-\frac{1}{2},1}]∪({2,+∞})$ | B. | $({-∞,-2}]∪({-1,-\frac{1}{2}}]∪({1,{{log}_2}3})$ | ||
| C. | $({-∞,-1}]∪({0,\frac{1}{2}}]∪({1,+∞})$ | D. | (-∞,-3]∪(-1,0]∪(1,log23) |
16.在极坐标系中,点(1,0)与点(2,π)的距离为( )
| A. | 1 | B. | 3 | C. | $\sqrt{1+{π^2}}$ | D. | $\sqrt{9+{π^2}}$ |
1.已知偶函数f(x)在[-1,0]上为单调增函数,则( )
| A. | f(sin$\frac{π}{8}$)<f(cos$\frac{π}{8}$) | B. | f(sin1)>f(cos1) | ||
| C. | f(sin$\frac{π}{12}$)<f(sin$\frac{5π}{12}$) | D. | f(sin$\frac{π}{12}$)>f(tan$\frac{π}{12}$) |
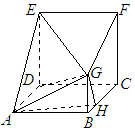 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH