题目内容
14．实数x，y，m，n满足．x2+y2+2x+2y-8=0．m2+n2+8m+8n+28=0，则（x-m）2+（y-n）2的最大值和最小值分别为（2+$\sqrt{10}$+3$\sqrt{2}$）2，0．分析 由题意化简可得圆的标准方程，从而作图象，而（x-m）2+（y-n）2的几何意义是两圆上的点的距离的平方，从而利用图象求解．
解答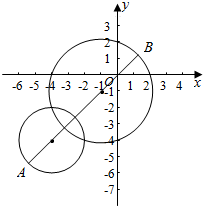 
解：∵x2+y2+2x+2y-8=0，
∴（x+1）2+（y+1）2=10，
∵m2+n2+8m+8n+28=0，
∴（m+4）2+（n+4）2=4；
作其图象如右图，
（x-m）2+（y-n）2的几何意义是两圆上的点的距离的平方，
|AB|=2+$\sqrt{10}$+3$\sqrt{2}$，
故（x-m）2+（y-n）2的最大值为（2+$\sqrt{10}$+3$\sqrt{2}$）2，
最小值为0．
故答案为：（2+$\sqrt{10}$+3$\sqrt{2}$）2，0．
点评 本题考查了数形结合的思想应用及学生的化简运算能力．
练习册系列答案
相关题目
2．若曲线y=x2在点（x0，x02）处切线的倾斜角为$\frac{π}{4}$，则x0=（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
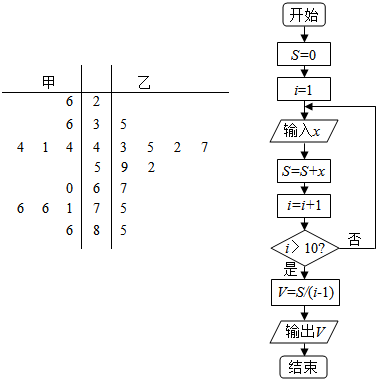为了调查网民对甲乙两个网站的关注度，随机抽取了甲乙两个网站9月份某10天在18：00～19：00时段内的点击量（单位：万次），整理后得到如下茎叶图．