题目内容
16.已知线段AB是半径为2的球O的直径,C,D两点在球O的球面上,CD=2,AB⊥CD,45°≤∠AOC≤135°,则四面体ABCD的体积的取值范围是$[\frac{4}{3},\frac{4\sqrt{3}}{3}]$.分析 判断棱锥体积取得最值的位置,求出四面体ABCD的体积的最值,即可得到范围.
解答 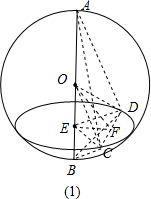 解:线段AB是半径为2的球O的直径,C,D两点在球O的球面上,CD=2,AB⊥CD,45°≤∠AOC≤135°,
解:线段AB是半径为2的球O的直径,C,D两点在球O的球面上,CD=2,AB⊥CD,45°≤∠AOC≤135°,
则四面体ABCD的体积的最小值是∠AOC=45°或135°时,经过CD与AB垂直的截面面积最小,如图(1)中三角形ECD,F为CD的中点,EC=OCsin45°=$\sqrt{2}$,OF=$\sqrt{3}$,EF=$\sqrt{({\sqrt{2})}^{2}-{1}^{2}}$
S△ECD=$\frac{1}{2}$CD•EF=$\frac{1}{2}×2×\sqrt{{(\sqrt{2})}^{2}-{1}^{2}}$=1.
棱锥体积的最小值为:$\frac{1}{3}×\frac{1}{2}×2×\sqrt{(\sqrt{2})^{2}-{1}^{2}}$×4=$\frac{4}{3}$.
当∠AOC=90°时,经过CD与AB垂直的截面面积最大,如图(2),截面三角形OCD是正三角形,边长为2.
棱锥体积的最大值为:$\frac{1}{3}×\frac{\sqrt{3}}{4}×{2}^{2}×4$=$\frac{4\sqrt{3}}{3}$.
四面体ABCD的体积的取值范围是:$[\frac{4}{3},\frac{4\sqrt{3}}{3}]$.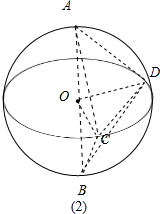
故答案为:$[\frac{4}{3},\frac{4\sqrt{3}}{3}]$.
点评 本题考查球的内接体,几何体的体积的最值的求法,考查空间想象能力以及计算能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.已知平面区域M={(x,y)|x2+y2≤4},N={(x,y)|$\left\{\begin{array}{l}{y≥mx+2m}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$},在区域M上随机取一点A,A落在区域N内的概率为P(N),若P(N)∈[$\frac{1}{2}$,$\frac{3π+2}{4π}$],则实数m的取值范围是( )
| A. | [0,1] | B. | [-$\frac{\sqrt{3}}{3}$,0] | C. | [-1,1] | D. | [-1,0] |
1.甲、乙两名射手在一次射击中得分为两个相互独立的随机变量X与Y,且X,Y的分布列为
(1)求a,b的值;
(2)计算X,Y的期望与方差,并以此分析甲、乙技术状况.
| X | 1 | 2 | 3 |
| P | a | 0.1 | 0.6 |
| Y | 1 | 2 | 3 |
| P | 0.3 | b | 0.3 |
(2)计算X,Y的期望与方差,并以此分析甲、乙技术状况.
8.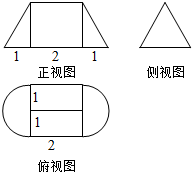 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
 一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )
一个几何体的侧视图是边长为2的正三角形,正视图与俯视图的尺寸如图所示,则此几何体的表面积为( )| A. | 12+2$\sqrt{3}$+3π | B. | 12+3π | C. | 2$\sqrt{3}$+$\frac{{\sqrt{3}π}}{3}$ | D. | 2$\sqrt{3}$+$\sqrt{3}$π |
