Question

6．已知平面区域M={（x，y）|x²+y²≤4}，N={（x，y）|$\left\{\begin{array}{l}{y≥mx+2m}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$}，在区域M上随机取一点A，A落在区域N内的概率为P（N），若P（N）∈[$\frac{1}{2}$，$\frac{3π+2}{4π}$]，则实数m的取值范围是（　　）

• A． [0，1]
• B． [-$\frac{\sqrt{3}}{3}$，0]
• C． [-1，1]
• D． [-1，0]

Answer 1

分析 画出图形，不难发现直线恒过定点（-2，0），结合概率范围可知直线与圆的关系，直线以（-2，0）点为中心顺时针旋转至与x轴重合，从而确定直线的斜率范围．

解答 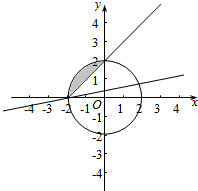解：画出图形，不难发现直线恒过定点（-2，0），
平面区域M={（x，y）|x²+y²≤4}，是圆及其内部，直线过（-2，0），（0，2）时，
它们围成的平面区域为M，向区域Ω上随机投一点A，
m=-1时，N={（x，y）|$\left\{\begin{array}{l}{y≥mx+2m}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$}的面积为3π+2，点A落在区域M内的概率为P（N），此时P（M）=$\frac{3π+2}{4π}$，
当直线与x轴重合时，P（N）=$\frac{1}{2}$；
直线的斜率范围是[-$\frac{\sqrt{3}}{3}$，0]．
故选：B．

点评 本题考查直线与圆的方程的应用，几何概型，直线系，数形结合的数学思想，是好题，难度较大．