题目内容

16．函数y=$\sqrt{2}sin（{x-{{45}°}}）-sinx$（　　）
A．是奇函数但不是偶函数B．是偶函数但不是奇函数
C．既是奇函数又是偶函数D．既不是奇函数又不是偶函数

分析 将函数化简，利用奇奇偶性的定义域判断即可．

解答 解：函数y=f（x）=$\sqrt{2}sin（{x-{{45}°}}）-sinx$=$\sqrt{2}$（$\frac{\sqrt{2}}{2}$sinx-$\frac{\sqrt{2}}{2}$cosx）-sinx=-cosx，
∵f（-x）=-cos（-x）=-cosx=f（x），
∴函数y=$\sqrt{2}sin（{x-{{45}°}}）-sinx$是偶函数．
故选B．

点评 本题主要考查三角函数的奇偶性的判断，利用三角函数公式将函数进行化简是解决本题的关键．

练习册系列答案
相关题目
6．已知$f（x）=2{cos^2}x+\sqrt{3}sin2x$，
（1）求函数f（x）的对称轴所在直线的方程；
（2）求函数f（x）的单调递增区间．
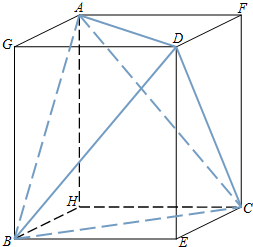7．如图，长宽高分别为a、b、c的长方体的六条面对角线组成等腰四面体ABCD．
（1）求证等腰四面体ABCD的每个面都是锐角三角形；
（2）求等腰四面体的体积及其外接球的表面积．
4．在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴建立极坐标系，直线l1的参数方程$\left\{\begin{array}{l}{x=2+\sqrt{2}t}\\{y=1+\sqrt{2}t}\end{array}\right.$（t是参数），直线l2的极坐标方程为ρ（cosθ+sinθ）=2，则l1与l2的夹角是90°．
11．传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数．他们研究过如图所示的三角形数，根据合情推理试猜测第七个三角形有（　　）个石子
A．28B．21C．36D．32
1．集合{1，2，3，…，n}（n≥3）中，每两个相异数作乘积，将所有这些乘积的和记为Tn，如：${T_3}=1×2+1×3+2×3=\frac{1}{2}[{6^2}-（{1^2}+{2^2}+{3^2}）]=11$；${T_4}=1×2+1×3+1×4+2×3+2×4+3×4=\frac{1}{2}[{10^2}-（{1^2}+{2^2}+{3^2}+{4^2}）]=35$；${T_5}=1×2+1×3+1×4+1×5+…+3×5+4×5=\frac{1}{2}[{15^2}-（{1^2}+{2^2}+{3^2}+{4^2}+{5^2}）]=85$
则T8=546．（写出计算结果）
8．已知一家公司生产某种品牌服装的年固定成本为10万元，每生产1千件需另投入3万元．设该公司一年内共生产该品牌服装x千件并全部销售完，每千件的销售收入为R（x）万元，且R（x）=$\left\{\begin{array}{l}{9.4-\frac{1}{30}{x}^{2}（0≤x≤10）}\\{\frac{110}{x}-\frac{432}{{x}^{2}}（x＞10）}\end{array}\right.$．
（1）写出年利润W（万元）关于年产量x（千件）的函数解析式；
（2）年产量为多少千件时，该公司在这一品牌服装的生产中所获得的年利润最大？
（注：年利润=年销售收入-年总成本）
5．已知函数f（x）=x3-3ax2+3a2x-a3（a∈R）的图象关于点（1，0）成中心对称．
（1）确定f（x）的解析式；
（2）求函数g（x）=f（x）-2x2在[-1，1]上的最大值和最小值．
6．如图，线段AB在平面α内，线段AC⊥α，线段BD⊥AB，且AB=1，AC=BD=4，BD与α所成角的正弦值为$\frac{1}{4}$，则CD=（　　）
A．5B．$\frac{11}{2}$C．6D．7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网